Typescript 와 fp-ts 라이브러리를 활용한 함수형 프로그래밍

정의

category 의 정의는 그렇게 복잡하진 않지만, 조금 길기 때문에 두 부분으로 나누겠습니다:

• 첫 번째는 단지 기술적인 것입니다 (구성요소를 정의할 필요가 있습니다)
• 두 번째는 우리가 관심있는 합성에 더 연관되어 있습니다

첫 번째 (구성요소)

category 는 (Objects, Morphisms) 쌍으로 되어있고 각각 다음을 의미합니다:

• Objects 는 object 들의 목록입니다
• Morphisms 는 object 들 간의 morphisms 의 목록 ("arrow" 라고도 불립니다) 입니다

참고. "object" 라는 용어는 프로그래밍에서의 "객체" 와는 관련이 없습니다. 단지 "object" 를 확인할 수 없는 블랙박스나, 다양한 morphisms 을 정의하는데 유용한 단순한 placeholder 라고 생각해주세요.

모든 morphisms f 는 원천 object A 와 대상 object B 를 가지고 있습니다.

모든 morphism 에서, A 와 B 는 모두 Ojbects 의 구성원입니다. 보통 f: A ⟼ B 라고 쓰며 "f 는 A 에서 B 로 가는 morphism" 이라 말합니다.

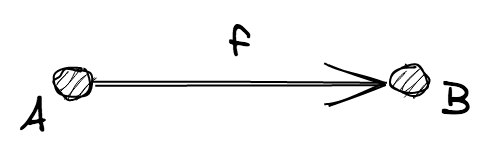
참고. 앞으로는, 단순하게 원은 제외하고 object 에만 라벨을 붙이겠습니다>

두 번째 (합성)

다음 속성을 만족하는 "합성" 이라 불리는 ∘ 연산이 존재합니다:

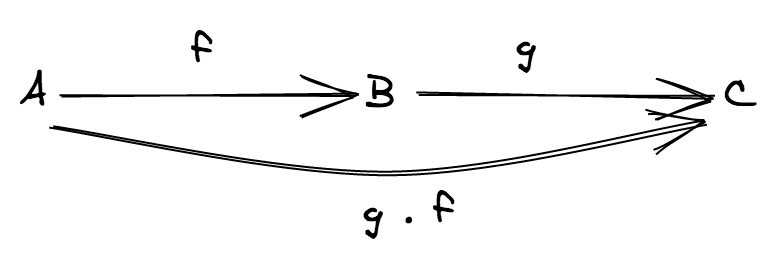
• (morphisms 의 합성) 모든 임의의 두 morphisms f: A ⟼ B 와 g: B ⟼ C 에 대해 f 와 g 의 합성 인 다음 g ∘ f: A ⟼ C morphism 이 존재해야 합니다.

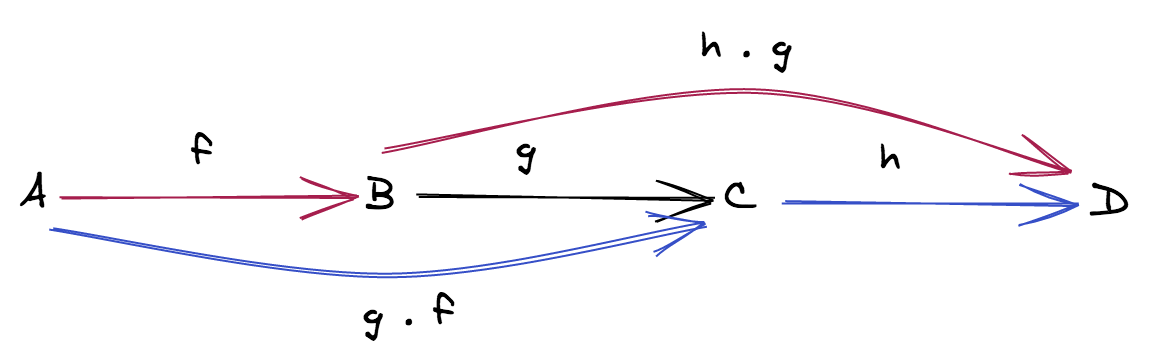
• (결합 법칙) 만약 f: A ⟼ B, g: B ⟼ C 이고 h: C ⟼ D 이면 h ∘ (g ∘ f) = (h ∘ g) ∘ f

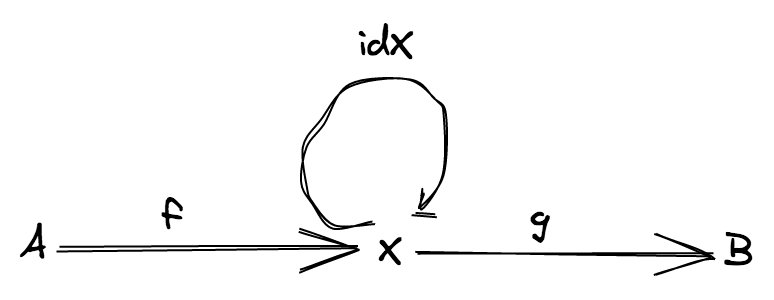
• (항등성) 모든 X 의 object 에 대해, 다음 법칙을 만족하는 identity morphism 이라 불리는 morphism identity: X ⟼ X 가 존재합니다. 모든 임의의 morphism f: A ⟼ X 와 g: X ⟼ B 에 대해, identity ∘ f = f 와 g ∘ identity = g 식을 만족합니다.

예제

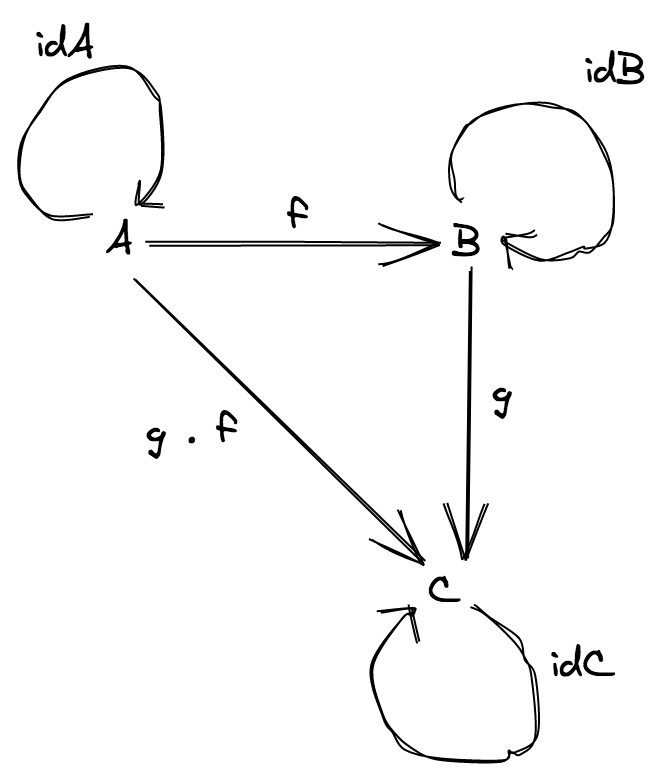
category 는 매우 단순합니다, 3 개의 objects 와 6 개의 morphism 이 존재합니다 (1A, 1B, 1C 와 A, B, C 에 대한 identity morphism 들 입니다).