Monad 정의

정의. Monad 는 다음 세 가지 항목으로 정의합니다:

(1) Functor 인스턴스를 만족하는 type constructor M

(2) 다음 시그니처를 가진 (pure 나 return 으로도 불리는) 함수 of:

of: <A>(a: A) => M<A>

(3) 다음 시그니처를 가진 (flatMap 이나 bind 로도 불리는) 함수 chain:

chain: <A, B>(f: (a: A) => M<B>) => (ma: M<A>) => M<B>

of 와 chain 함수는 아래 세 가지 법칙을 만족해야 합니다:

  • chain(of) ∘ f = f (좌동등성)
  • chain(f) ∘ of = f (우동등성)
  • chain(h) ∘ (chain(g) ∘ f) = chain((chain(h) ∘ g)) ∘ f (결합법칙)

여기서 f, g, h 는 모두 effectful 함수이며 ∘ 는 보통의 함수 합성을 말합니다.

처음 이 정의를 보았을 때 많은 의문이 생겼습니다:

  • of 와 chain 연산이란 무엇인가? 왜 그러한 시그니처를 가지고 있는가?
  • 왜 "pure" 나 "flatMap" 와 같은 동의어를 가지고 있는가?
  • 왜 그러한 법칙을 만족해야 하는가? 그것은 무엇을 의미하는가?
  • flatten 이 monad 에서 그렇게 중요하다면, 왜 정의에는 보이지 않는걸까?

이번 장에서 위 의문들을 모두 해소할 것입니다.

핵심 문제로 돌아가봅시다: 두 effectful 함수 f 와 g 의 합성이란 무엇일까요?

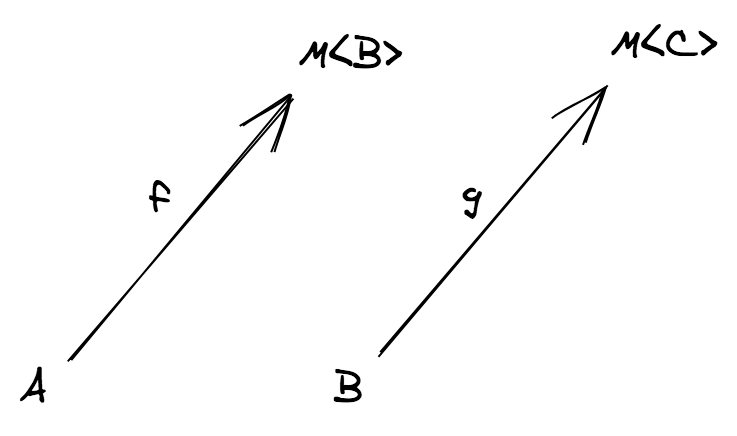
two Kleisli arrows, what's their composition?

참고. Effectful 함수는 Kleisli arrow 라고도 불립니다.

당분간은 그러한 합성의 타입 조차 알지 못합니다.

하지만 우리는 이미 합성에 대해 구체적으로 이야기하는 추상적인 개념들을 살펴보았습니다. 우리가 category 에 대해 말했던 것을 기억하나요?

category 는 합성의 본질이라 할 수 있습니다.

우리는 당면한 문제를 category 문제로 바꿀 수 있습니다: Kleisli arrows 의 합성을 모델링하는 category 를 찾을 수 있을까요?