Semigroup 의 정의
어떤
Magma의concat연산이 결합법칙을 만족하면 semigroup 이다.
여기서 "결합법칙" 은 A 의 모든 x, y, z 에 대해 다음 등식이 성립하는 것을 의미합니다:
(x * y) * z = x * (y * z)
// or
concat(concat(a, b), c) = concat(a, concat(b, c))
쉽게 말하면 _결합법칙_은 표현식에서 괄호를 신경쓸 필요없이 단순히 x * y * z 로 쓸 수 있다는 사실을 알려줍니다.
예제
문자열 연결은 결합법칙을 만족합니다.
("a" + "b") + "c" = "a" + ("b" + "c") = "abc"
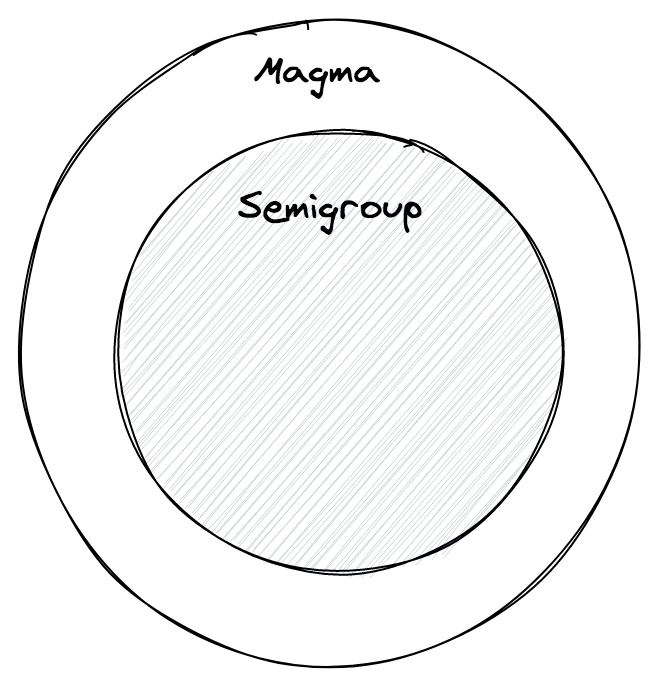
모든 semigroup 은 magma 입니다, 하지만 모든 magma 가 semigroup 인것은 아닙니다.
예제
이전 예제 MagmaSub 는 concat 이 결합법칙을 만족하지 않기에 semigroup 이 아닙니다.
import { pipe } from 'fp-ts/function'
import { Magma } from 'fp-ts/Magma'
const MagmaSub: Magma<number> = {
concat: (first, second) => first - second
}
pipe(MagmaSub.concat(MagmaSub.concat(1, 2), 3), console.log) // => -4
pipe(MagmaSub.concat(1, MagmaSub.concat(2, 3)), console.log) // => 2
Semigroup 은 병렬 연산이 가능하다는 의미를 내포합니다
(원문) Semigroups capture the essence of parallelizable operations
어떤 계산이 결합법칙을 만족한다는 것을 안다면, 계산을 두 개의 하위 계산으로 더 분할할 수 있고, 각각의 계산은 하위 계산으로 더 분할될 수 있습니다.
a * b * c * d * e * f * g * h = ((a * b) * (c * d)) * ((e * f) * (g * h))
하위 계산은 병렬로 실행할 수 있습니다.
Magga 처럼, Semigroup 도 Typescript interface 로 정의할 수 있습니다:
// fp-ts/lib/Semigroup.ts
interface Semigroup<A> extends Magma<A> {}
다음 법칙을 만족해야 합니다:
- 결합법칙: 만약
S가 semigroup 이면 타입A의 모든x,y,z에 대해 다음 등식이 성립합니다
S.concat(S.concat(x, y), z) = S.concat(x, S.concat(y, z))
참고. 안타깝게도 Typescript 의 타입시스템 만으론 이 법칙을 강제할 수 없습니다.
ReadonlyArray<string> 에 대한 semigroup 을 구현해봅시다:
import * as Se from 'fp-ts/Semigroup'
const Semigroup: Se.Semigroup<ReadonlyArray<string>> = {
concat: (first, second) => first.concat(second)
}
concat 이란 이름은 (이후 알게 되겠지만) 배열에 대해서는 적절합니다. 하지만 인스턴스를 만드려는 타입 A 와 문맥에 따라, concat 연산은 아래와 같은 다른 해석과 의미를 가질 수 있습니다.
(원문) The name
concatmakes sense for arrays (as we'll see later) but, depending on the context and the typeAon whom we're implementing an instance, theconcatsemigroup operation may have different interpretations and meanings:
- "concatenation"
- "combination"
- "merging"
- "fusion"
- "selection"
- "sum"
- "substitution"
예제
다음은 semigroup (number, +) 을 정의한 것입니다. 여기서 + 는 숫자에 대한 덧셈을 의미합니다:
import { Semigroup } from 'fp-ts/Semigroup'
/** 덧셈에 대한 number `Semigroup` */
const SemigroupSum: Semigroup<number> = {
concat: (first, second) => first + second
}
문제. 이전 데모 의 01_retry.ts 에 정의된 concat combinator 를 RetryPolicy 타입에 대한 Semigroup 인스턴스로 정의할 수 있을까요?
다음은 semigroup (number, *) 을 정의한 것입니다. 여기서 * 는 숫자에 대한 덧셈을 의미합니다:
import { Semigroup } from 'fp-ts/Semigroup'
/** 곱셈에 대한 number `Semigroup` */
const SemigroupProduct: Semigroup<number> = {
concat: (first, second) => first * second
}
참고 흔히 number 의 semigroup 에 한정지어 생각하곤 하지만, 임의의 타입 A 에 대해 다른 Semigroup<A> 인스턴스를 정의하는 것도 가능합니다. number 타입의 덧셈 과 곱셈 연산에 대한 semigroup 을 정의한것처럼 다른 타입에 대해 같은 연산으로 Semigroup 을 만들 수 있습니다. 예들들어 SemigoupSum 은 number 와 같은 타입대신 자연수에 대해서도 구현할 수 있습니다.
(원문) It is a common mistake to think about the semigroup of numbers, but for the same type
Ait is possible to define more instances ofSemigroup<A>. We've seen how fornumberwe can define a semigroup under addition and multiplication. It is also possible to haveSemigroups that share the same operation but differ in types.SemigroupSumcould've been implemented on natural numbers instead of unsigned floats likenumber.
string 타입에 대한 다른 예제입니다:
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupString: Semigroup<string> = {
concat: (first, second) => first + second
}
이번에는 boolean 타입에 대한 또 다른 2개의 에제입니다:
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupAll: Semigroup<boolean> = {
concat: (first, second) => first && second
}
const SemigroupAny: Semigroup<boolean> = {
concat: (first, second) => first || second
}