Monoids 를 통한 합성 모델링

지금까지 배운것을 다시 정리해봅시다.

대수이 아래 조합으로 이루어져 있다는 것을 보았습니다:

타입 A
타입 A 와 연관된 몇가지 연산들
조합을 위한 몇가지 법칙과 속성

처음 살펴본 대수는 concat 으로 불리는 연산을 하나 가진 magma 였습니다. Magma<A> 에 대한 특별한 법칙은 없었고 다만 concat 연산이 A 에 대해 닫혀있어야 했습니다. 즉 다음 연산의 결과는

concat(first: A, second: A) => A

여전히 A 에 속해야 합니다.

이후 여기에 하나의 간단한 결합법칙 을 추가함으로써, Magma<A> 를 더 다듬어진 Semigroup<A> 을 얻게 되었습니다. 이를 통해 결합법칙이 병렬계산을 가능하게 해주는지 알게 되었습니다.

이제 Semigroup 에 또 다른 규칙을 추가하고자 합니다.

concat 연산이 있는 집합 A 에 대한 Semigorup 이 주어진 경우, 만약 집합 A 의 어떤 한 요소가 A 의 모든 요소 a 에 대해 다음 두 조건을 만족한다면 (이 요소를 empty 라 부르겠습니다)

우동등성(Right identity): concat(a, empty) = a
좌동등성(Left identity): concat(empty, a) = a

이 Semigroup 은 또한 Moniod 입니다.

참고: 이후 내용에서는 empty 를 unit 으로 부르겠습니다. 다른 여러 동의어들이 있으며, 그 중 가장 많이 쓰이는 것은 neutral element 과 identity element 입니다.

import { Semigroup } from 'fp-ts/Semigroup'

interface Monoid<A> extends Semigroup<A> {
  readonly empty: A
}

이전까지 본 많은 semigroup 들이 Monid 로 확장할 수 있었습니다. A 에 대해 우동등성과 좌동등성을 만족하는 요소를 찾기만 하면 됩니다.

import { Monoid } from 'fp-ts/Monoid'

/** 덧셈에 대한 number `Monoid` */
const MonoidSum: Monoid<number> = {
  concat: (first, second) => first + second,
  empty: 0
}

/** 곰셈에 대한 number `Monoid` */
const MonoidProduct: Monoid<number> = {
  concat: (first, second) => first * second,
  empty: 1
}

const MonoidString: Monoid<string> = {
  concat: (first, second) => first + second,
  empty: ''
}

/** 논리곱에 대한 boolean monoid */
const MonoidAll: Monoid<boolean> = {
  concat: (first, second) => first && second,
  empty: true
}

/** 논리합에 대한 boolean monoid */
const MonoidAny: Monoid<boolean> = {
  concat: (first, second) => first || second,
  empty: false
}

문제. 이전 섹션에서 타입 ReadonlyArray<string> 에 대한 Semigorup 인스턴스를 정의했습니다:

import { Semigroup } from 'fp-ts/Semigroup'

const Semigroup: Semigroup<ReadonlyArray<string>> = {
  concat: (first, second) => first.concat(second)
}

이 semigroup 에 대한 unit 을 찾을 수 있을까요? 만약 그렇다면, ReadonlyArray<string> 뿐만 아니라 ReadonlyArray<A> 에 대해서도 그렇다고 일반화할 수 있을까요?

문제 (더 복잡함). 임의의 monoid 에 대해, unit 이 오직 하나만 있음을 증명해보세요.

위 증명을 통해 monoid 당 오직 하나의 unit 만 있다는 것이 보증되기에, 우리는 monoid 에서 unit 을 하나 찾았다면 더 이상 찾지 않아도 됩니다.

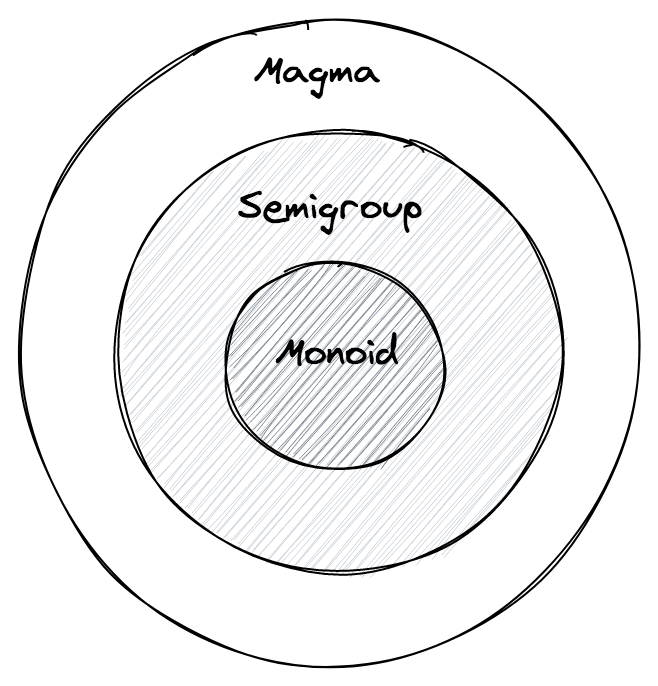
모든 semigroup 은 magma 이지만, 역은 성립하지 않았듯이, 모든 monoid 는 semigroup 이지만, 모든 semigroup 이 monoid 는 아닙니다.

Magma vs Semigroup vs Monoid

예제

다음 예제를 살펴봅시다:

import { pipe } from 'fp-ts/function'
import { intercalate } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'

const SemigroupIntercalate = pipe(S.Semigroup, intercalate('|'))

console.log(S.Semigroup.concat('a', 'b')) // => 'ab'
console.log(SemigroupIntercalate.concat('a', 'b')) // => 'a|b'
console.log(SemigroupIntercalate.concat('a', '')) // => 'a|'

이 semigroup 은 concat(a, empty) = a 를 만족하는 string 타입인 empty 가 존재하지 않는점을 확인해주세요.

마지막으로, 함수가 포함된 더 "난해한" 예제입니다:

예제

endomorphism 은 입력과 출력 타입이 같은 함수를 말합니다:

type Endomorphism<A> = (a: A) => A

임의의 타입 A 에 대해, A 의 endomorphism 에 대해 다음과 같이 정의된 인스턴스는 monoid 입니다:

concat 연산은 일반적인 함수 합성과 같습니다
unit 값은 항등함수 입니다

import { Endomorphism, flow, identity } from 'fp-ts/function'
import { Monoid } from 'fp-ts/Monoid'

export const getEndomorphismMonoid = <A>(): Monoid<Endomorphism<A>> => ({
  concat: flow,
  empty: identity
})

참고: identity 함수는 다음과 같은 구현 하나만 존재합니다:

const identity = (a: A) => a

입력으로 무엇을 받든지, 그것을 그대로 결과로 돌려줍니다.

Typescript 와 fp-ts 라이브러리를 활용한 함수형 프로그래밍

Monoids 를 통한 합성 모델링