소개
이 저장소는 Typescript 와 fp-ts 라이브러리를 활용한 함수형 프로그래밍을 소개합니다.
모든 내용은 enricopolanski 의 저장소에서 나온 것입니다.
해당 저장소도 이탈리아어로 작성된 Giulio Canti 의 "Introduction to Functional Programming (Italian)" 을 영어로 번역한 것입니다.
원본 작성자는 해당 글을 함수형 프로그래밍에 관한 강의나 워크샵에 참고자료로 사용하였습니다.
개인적인 공부와 fp-ts 라이브러리 생태계를 소개하기 위한 목적으로 번역하였습니다.
오역 및 번역이 매끄럽지 않은 부분이 존재하며 특히 번역이 어려웠던 부분은 원글을 함께 표시하였습니다.
Setup
git clone https://github.com/jbl428/functional-programming.git
cd functional-programming
npm i
함수형 프로그래밍이란
함수형 프로그래밍은 순수함수, 수학적인 함수를 사용하는 프로그래밍입니다.
인터넷 검색을 통해서 아마 다음과 같은 정의를 볼 수 있습니다:
(순수) 함수란 같은 입력에 항상 같은 결과를 내는 부작용없는 절차입니다.
여기서 "부작용" 이란 용어의 정의를 설명하지 않았지만 (이후 공식적인 정의를 보게될것입이다) 직관적으로 파일을 열거나 데이터베이스의 쓰기같은 것을 생각해볼 수 있습니다.
지금 당장은 부작용이란 함수가 값을 반환하는 작업 이외에 하는 모든것이라고 생각하시면 됩니다.
순수함수만 사용하는 프로그램은 어떤 구조를 가질까요?
보통 함수형 프로그램은 pipeline 형태로 이루어져 있습니다.
const program = pipe(
input,
f1, // 순수 함수
f2, // 순수 함수
f3, // 순수 함수
...
)
여기서 input은 첫 번째 함수인 f1으로 전달되고 그 결과는 두 번째 함수인 f2로 전달됩니다.
이어서 f2가 반환하는 값은 세 번째 함수인 f3로 전달되고 이후 같은 방식으로 진행됩니다.
데모
앞으로 함수형 프로그래밍이 위와 같은 구조를 만들어주는 도구를 제공하는지 보게될 것입니다.
함수형 프로그래밍이 무엇인지 이해하는 것 외에 이것의 궁극적인 목적을 이해하는 것 또한 중요합니다.
함수형 프로그래밍의 목적은 수학적인 모델 을 사용해 시스템의 복잡성을 조정하고 코드의 속성 과 리팩토링의 편의성에 중점을 두는 것입니다.
(원문) Functional programming's goal is to tame a system's complexity through the use of formal models, and to give careful attention to code's properties and refactoring ease.
함수형 프로그래밍은 프로그램 구조에 감춰진 수학을 사람들에게 가르치는 것에 도와줍니다:
- 합성 가능한 코드를 작성하는법
- 부작용을 어떻게 다루는지
- 일관적이고 범용적이며 체계적인 API 를 만드는 법
코드의 속성에 중점을 둔다는 것이 무엇일까요? 예제를 살펴보겠습니다:
예제
왜 for반복문보다 Array의 map이 더 함수형이라고 할까요?
// 입력
const xs: Array<number> = [1, 2, 3]
// 수정
const double = (n: number): number => n * 2
// 결과: `xs` 의 각 요소들이 2배가 된 배열을 얻고싶다
const ys: Array<number> = []
for (let i = 0; i <= xs.length; i++) {
ys.push(double(xs[i]))
}
for반복문은 많은 유연성을 제공합니다. 즉 다음 값들을 수정할 수 있습니다.
- 시작 위치,
let i = 0 - 반복 조건,
i < xs.length - 반복 제어,
i++.
이는 에러를 만들어 낼 수 있음을 의미하며 따라서 결과물에 대한 확신이 줄어듭니다.
문제. 위 for 반복문은 올바른가요?
위 예제를 map을 활용해 작성해봅시다.
// 입력
const xs: Array<number> = [1, 2, 3]
// 수정
const double = (n: number): number => n * 2
// 결과: `xs` 의 각 요소들이 2배가 된 배열을 얻고싶다
const ys: Array<number> = xs.map(double)
map은 for 반복문에 비해 유연성이 적지만 다음과 같은 확신을 제공합니다.
- 입력 배열의 모든 요소에 대해 처리될것이다.
- 결과 배열의 크기는 입력 배열의 크기와 동일할 것이다.
함수형 프로그래밍에선 구체적인 구현보다 코드의 속성에 더 집중합니다.
즉 map 연산의 제약사항이 오히려 유용하게 해줍니다.
for 반복문 보다 map 을 사용한 PR 을 리뷰할 때 얼마나 편한지 생각해보세요.
함수형 프로그래밍의 두 가지 요소
함수형 프로그래밍은 다음 두 가지 요소를 기반으로 한다:
- 참조 투명성
- 합성 (범용적 디자인 패턴으로서)
이후 내용은 위 두가지 요소와 직간접적으로 연관되어 있습니다.
참조 투명성
정의. 표현식이 평가되는 결과로 바꿔도 프로그래밍의 동작이 변하지 않는다면 해당 표현식은 참조에 투명하다고 말합니다.
예제 (참조 투명성은 순수함수를 사용하는 것을 의미합니다)
const double = (n: number): number => n * 2
const x = double(2)
const y = double(2)
double(2) 표현식은 그 결과인 4로 변경할 수 있기에 참조 투명성을 가지고 있습니다.
따라서 코드를 아래와 같이 바꿀 수 있습니다.
const x = 4
const y = x
모든 표현식이 항상 참조 투명하지는 않습니다. 다음 예제를 봅시다.
예제 (참조 투명성은 에러를 던지지 않는것을 의미합니다)
const inverse = (n: number): number => {
if (n === 0) throw new Error('cannot divide by zero')
return 1 / n
}
const x = inverse(0) + 1
inverse(0) 는 참조 투명하지 않기 때문에 결과로 대체할 수 없습니다.
예제 (참조 투명성을 위해 불변 자료구조를 사용해야 합니다)
const xs = [1, 2, 3]
const append = (xs: Array<number>): void => {
xs.push(4)
}
append(xs)
const ys = xs
마지막 라인에서 xs 는 초기값인 [1, 2, 3] 으로 대체할 수 없습니다. 왜냐하면 append 함수를 호출해 값이 변경되었기 때문입니다.
왜 참조 투명성이 중요할까요? 다음과 같은 것을 얻을 수 있기 때문입니다:
- 지역적인 코드분석 코드를 이해하기 위해 외부 문맥을 알 필요가 없습니다
- 코드 수정 시스템의 동작을 변경하지 않고 코드를 수정할 수 있습니다
문제. 다음과 같은 프로그램이 있다고 가정합시다:
// Typescript 에서 `declare` 를 사용하면 함수의 구현부 없이 선언부만 작성할 수 있습니다
declare const question: (message: string) => Promise<string>
const x = await question('What is your name?')
const y = await question('What is your name?')
다음과 같이 코드를 수정해도 괜찮을까요? 프로그램 동작이 변할까요?
const x = await question('What is your name?')
const y = x
보시다시피 참조 투명하지 않은 표현식을 수정하는 것은 매우 어렵습니다. 모든 표현식이 참조 투명한 함수형 프로그램에선 수정에 필요한 인지 부하를 상당히 줄일 수 있습니다.
(원문) In functional programming, where every expression is referentially transparent, the cognitive load required to make changes is severely reduced.
합성
함수형 프로그래밍의 기본 패턴은 합성입니다: 특정한 작업을 수행하는 작은 단위의 코드를 합성해 크고 복잡한 단위로 구성합니다.
"가장 작은것에서 가장 큰것으로" 합성하는 패턴의 예로 다음과 같은 것이 있습니다:
- 두 개 이상의 기본타입 값을 합성 (숫자나 문자열)
- 두 개 이상의 함수를 합성
- 전체 프로그램의 합성
마지막 예는 모듈화 프로그래밍 이라 할 수 있습니다:
모듈화 프로그래밍이란 더 작은 프로그램을 붙여 큰 프로그램을 만드는 과정을 의미한다 - Simon Peyton Jones
이러한 프로그래밍 스타일은 combinator 를 통해 이루어집니다.
여기서 combinator 는 combinator pattern 에서 말하는 용어입니다.
사물들을 조합한다는 개념을 중심으로 하여 라이브러리를 만드는 방법. 보통 어떤 타입
T와T의 기본값들, 그리고T의 값들을 다양한 방법으로 조합해 더 복잡한 값을 만든는 "combinator" 가 있습니다.(원문) A style of organizing libraries centered around the idea of combining things. Usually there is some type
T, some "primitive" values of typeT, and some "combinators" which can combine values of typeTin various ways to build up more complex values of typeT
combinator 의 일반적인 개념은 다소 모호하고 다른 형태로 나타날 수 있지만, 가장 간단한 것은 다음과 같다:
combinator: Thing -> Thing
예제. double 함수는 두 수를 조합합니다.
combinator 의 목적은 이미 정의된 어떤 것으로 부터 새로운 어떤 것을 만드는 것입니다.
combinator 의 출력인 새로운 어떤 것은 다른 프로그램이나 combinator 로 전달할 수 있기 때문에, 우리는 조합적 폭발을 얻을 수 있으며 이는 이 패턴이 매우 강력하다는 것을 의미합니다.
(원문) Since the output of a combinator, the new Thing, can be passed around as input to other programs and combinators, we obtain a combinatorial explosion of opportunities, which makes this pattern extremely powerful.
예제
import { pipe } from 'fp-ts/function'
const double = (n: number): number => n * 2
console.log(pipe(2, double, double, double)) // => 16
따라서 함수형 모듈에서 다음과 같은 일반적인 형태를 볼 수 있습니다:
- 타입
T에 대한 model - 타입
T의 "primitives" - primitives 를 더 큰 구조로 조합하기 위한 combinators
이와 같은 모듈을 만들어봅시다.
데모
위 데모를 통해 알 수 있듯이, 3개의 primitive 와 2 개의 combinator 만으로도 꽤 복잡한 정책을 표현할 수 있었습니다.
만약 새로운 primitive 나 combinator 를 기존것들과 조합한다면 표현가능한 경우의 수가 기하급수적으로 증가하는 것을 알 수 있습니다.
01_retry.ts에 있는 두 개의 combinator 에서 특히 중요한 함수는 concat인데 강력한 함수형 프로그래밍 추상화인 semigroup 과 관련있기 때문입니다.
Semigroup 으로 합성 모델링
semigroup 은 두 개 이상의 값을 조합하는 설계도입니다.
semigroup 은 대수 (algebra) 이며, 다음과 같은 조합으로 정의됩니다.
- 하나 이상의 집합
- 해당 집합에 대한 하나 이상의 연산
- 이전 연산에 대한 0개 이상의 법칙
대수학은 수학자들이 어떤 개념을 불필요한 모든 것을 제거한 가장 순수한 형태로 만드려는 방법입니다.
대수는 자신의 법칙에 따라 대수 그 자체로 정의되는 연산에 의해서만 변경이 허용된다.
(원문) When an algebra is modified the only allowed operations are those defined by the algebra itself according to its own laws
대수학은 인터페이스 의 추상화로 생각할 수 있습니다.
인터페이스는 자신의 법칙에 따라 인터페이스 그 자체로 정의되는 연산에 의해서만 변경이 허용된다.
(원문) When an interface is modified the only allowed operations are those defined by the interface itself according to its own laws
semigroups 에 대해 알아보기 전에, 첫 대수의 예인 magma 를 살펴봅시다.
Magma 의 정의
Magma<A> 는 매우 간단한 대수입니다:
- 타입 (A) 의 집합
concat연산- 지켜야 할 법칙은 없음
참고: 대부분의 경우 set 과 type 은 같은 의미로 사용됩니다.
Magma 를 정의하기 위해 Typescript 의 interface 를 활용할 수 있습니다.
interface Magma<A> {
readonly concat: (first: A, second: A) => A
}
이를통해, 대수를 위한 재료를 얻게됩니다.
- 집합
A - 집합
A에 대한 연산인concat. 이 연산은 집합A에 대해 닫혀있다 고 말합니다. 임의의A요소에 대해 연산의 결과도 항상A이며 이 값은 다시concat의 입력으로 쓸 수 있습니다.concat은 다른 말로 타입A의combinator입니다.
Magma<A> 의 구체적인 인스턴스 하나를 구현해봅니다. 여기서 A 는 number 입니다.
import { Magma } from 'fp-ts/Magma'
const MagmaSub: Magma<number> = {
concat: (first, second) => first - second
}
// helper
const getPipeableConcat = <A>(M: Magma<A>) => (second: A) => (first: A): A =>
M.concat(first, second)
const concat = getPipeableConcat(MagmaSub)
// 사용 예제
import { pipe } from 'fp-ts/function'
pipe(10, concat(2), concat(3), concat(1), concat(2), console.log)
// => 2
문제. 위 concat 이 닫힌 연산이라는 점은 쉽게 알 수 있습니다. 만약 A JavaScript 의 number(양수와 음수 float 집합)가 아닌 가 자연수의 집합(양수로 정의된) 이라면, MagmaSub 에 구현된 concat 과 같은 연산을 가진 Magma<Natural> 을 정의할 수 있을까요? 자연수에 대해 닫혀있지 않는 또다른 concat 연산을 생각해 볼 수 있나요?
정의. 주어진 A 가 공집합이 아니고 이항연산 * 가 A 에 대해 닫혀있다면, 쌍 (A, *) 를 _magma_라 합니다.
Magma 는 닫힘 조건외에 다른 법칙을 요구하지 않습니다. 이제 semigroup 이라는 추가 법칙을 요구하는 대수를 살펴봅시다.
Semigroup 의 정의
어떤
Magma의concat연산이 결합법칙을 만족하면 semigroup 이다.
여기서 "결합법칙" 은 A 의 모든 x, y, z 에 대해 다음 등식이 성립하는 것을 의미합니다:
(x * y) * z = x * (y * z)
// or
concat(concat(a, b), c) = concat(a, concat(b, c))
쉽게 말하면 _결합법칙_은 표현식에서 괄호를 신경쓸 필요없이 단순히 x * y * z 로 쓸 수 있다는 사실을 알려줍니다.
예제
문자열 연결은 결합법칙을 만족합니다.
("a" + "b") + "c" = "a" + ("b" + "c") = "abc"
모든 semigroup 은 magma 입니다, 하지만 모든 magma 가 semigroup 인것은 아닙니다.
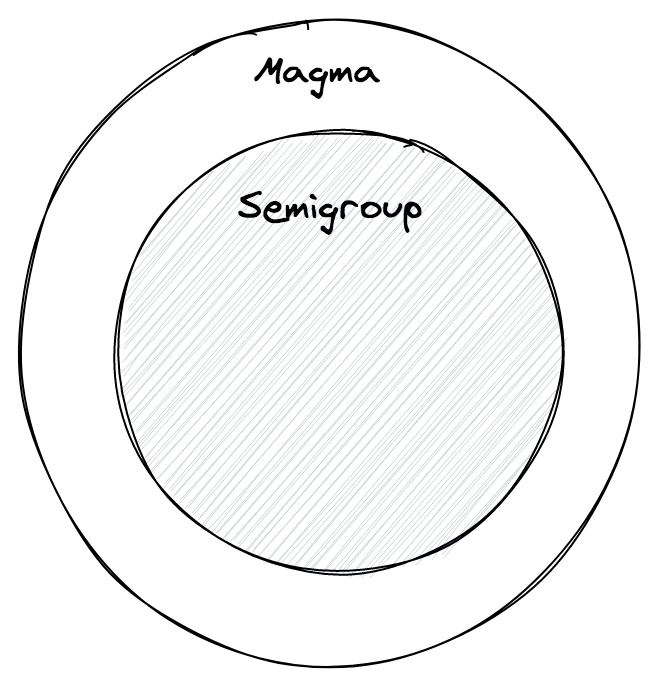
예제
이전 예제 MagmaSub 는 concat 이 결합법칙을 만족하지 않기에 semigroup 이 아닙니다.
import { pipe } from 'fp-ts/function'
import { Magma } from 'fp-ts/Magma'
const MagmaSub: Magma<number> = {
concat: (first, second) => first - second
}
pipe(MagmaSub.concat(MagmaSub.concat(1, 2), 3), console.log) // => -4
pipe(MagmaSub.concat(1, MagmaSub.concat(2, 3)), console.log) // => 2
Semigroup 은 병렬 연산이 가능하다는 의미를 내포합니다
(원문) Semigroups capture the essence of parallelizable operations
어떤 계산이 결합법칙을 만족한다는 것을 안다면, 계산을 두 개의 하위 계산으로 더 분할할 수 있고, 각각의 계산은 하위 계산으로 더 분할될 수 있습니다.
a * b * c * d * e * f * g * h = ((a * b) * (c * d)) * ((e * f) * (g * h))
하위 계산은 병렬로 실행할 수 있습니다.
Magga 처럼, Semigroup 도 Typescript interface 로 정의할 수 있습니다:
// fp-ts/lib/Semigroup.ts
interface Semigroup<A> extends Magma<A> {}
다음 법칙을 만족해야 합니다:
- 결합법칙: 만약
S가 semigroup 이면 타입A의 모든x,y,z에 대해 다음 등식이 성립합니다
S.concat(S.concat(x, y), z) = S.concat(x, S.concat(y, z))
참고. 안타깝게도 Typescript 의 타입시스템 만으론 이 법칙을 강제할 수 없습니다.
ReadonlyArray<string> 에 대한 semigroup 을 구현해봅시다:
import * as Se from 'fp-ts/Semigroup'
const Semigroup: Se.Semigroup<ReadonlyArray<string>> = {
concat: (first, second) => first.concat(second)
}
concat 이란 이름은 (이후 알게 되겠지만) 배열에 대해서는 적절합니다. 하지만 인스턴스를 만드려는 타입 A 와 문맥에 따라, concat 연산은 아래와 같은 다른 해석과 의미를 가질 수 있습니다.
(원문) The name
concatmakes sense for arrays (as we'll see later) but, depending on the context and the typeAon whom we're implementing an instance, theconcatsemigroup operation may have different interpretations and meanings:
- "concatenation"
- "combination"
- "merging"
- "fusion"
- "selection"
- "sum"
- "substitution"
예제
다음은 semigroup (number, +) 을 정의한 것입니다. 여기서 + 는 숫자에 대한 덧셈을 의미합니다:
import { Semigroup } from 'fp-ts/Semigroup'
/** 덧셈에 대한 number `Semigroup` */
const SemigroupSum: Semigroup<number> = {
concat: (first, second) => first + second
}
문제. 이전 데모 의 01_retry.ts 에 정의된 concat combinator 를 RetryPolicy 타입에 대한 Semigroup 인스턴스로 정의할 수 있을까요?
다음은 semigroup (number, *) 을 정의한 것입니다. 여기서 * 는 숫자에 대한 덧셈을 의미합니다:
import { Semigroup } from 'fp-ts/Semigroup'
/** 곱셈에 대한 number `Semigroup` */
const SemigroupProduct: Semigroup<number> = {
concat: (first, second) => first * second
}
참고 흔히 number 의 semigroup 에 한정지어 생각하곤 하지만, 임의의 타입 A 에 대해 다른 Semigroup<A> 인스턴스를 정의하는 것도 가능합니다. number 타입의 덧셈 과 곱셈 연산에 대한 semigroup 을 정의한것처럼 다른 타입에 대해 같은 연산으로 Semigroup 을 만들 수 있습니다. 예들들어 SemigoupSum 은 number 와 같은 타입대신 자연수에 대해서도 구현할 수 있습니다.
(원문) It is a common mistake to think about the semigroup of numbers, but for the same type
Ait is possible to define more instances ofSemigroup<A>. We've seen how fornumberwe can define a semigroup under addition and multiplication. It is also possible to haveSemigroups that share the same operation but differ in types.SemigroupSumcould've been implemented on natural numbers instead of unsigned floats likenumber.
string 타입에 대한 다른 예제입니다:
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupString: Semigroup<string> = {
concat: (first, second) => first + second
}
이번에는 boolean 타입에 대한 또 다른 2개의 에제입니다:
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupAll: Semigroup<boolean> = {
concat: (first, second) => first && second
}
const SemigroupAny: Semigroup<boolean> = {
concat: (first, second) => first || second
}
concatAll 함수
정의상 concat 은 단지 2개의 요소 A 를 조합합니다. 몇 개라도 조합이 가능할까요?
concatAll 함수는 다음 값을 요구합니다:
- semigroup 인스턴스
- 초기값
- 요소의 배열
import * as S from 'fp-ts/Semigroup'
import * as N from 'fp-ts/number'
const sum = S.concatAll(N.SemigroupSum)(2)
console.log(sum([1, 2, 3, 4])) // => 12
const product = S.concatAll(N.SemigroupProduct)(3)
console.log(product([1, 2, 3, 4])) // => 72
문제. 왜 초기값을 제공해야 할까요?
예제
Javascript 기본 라이브러리의 유명한 함수 몇가지를 concatAll 으로 구현해봅시다.
import * as B from 'fp-ts/boolean'
import { concatAll } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/struct'
const every = <A>(predicate: (a: A) => boolean) => (
as: ReadonlyArray<A>
): boolean => concatAll(B.SemigroupAll)(true)(as.map(predicate))
const some = <A>(predicate: (a: A) => boolean) => (
as: ReadonlyArray<A>
): boolean => concatAll(B.SemigroupAny)(false)(as.map(predicate))
const assign: (as: ReadonlyArray<object>) => object = concatAll(
S.getAssignSemigroup<object>()
)({})
문제. 다음 인스턴스는 semigroup 법칙을 만족합니까?
import { Semigroup } from 'fp-ts/Semigroup'
/** 항상 첫 번째 인자를 반환 */
const first = <A>(): Semigroup<A> => ({
concat: (first, _second) => first
})
문제. 다음 인스턴스는 semigroup 법칙을 만족합니까?
import { Semigroup } from 'fp-ts/Semigroup'
/** 항상 두 번째 인자를 반환 */
const last = <A>(): Semigroup<A> => ({
concat: (_first, second) => second
})
Dual semigroup
semigroup 인스턴스가 주어지면, 단순히 조합되는 피연산자의 순서를 변경해 새로운 semigroup 인스턴스를 얻을 수 있습니다.
import { pipe } from 'fp-ts/function'
import { Semigroup } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'
// Semigroup combinator
const reverse = <A>(S: Semigroup<A>): Semigroup<A> => ({
concat: (first, second) => S.concat(second, first)
})
pipe(S.Semigroup.concat('a', 'b'), console.log) // => 'ab'
pipe(reverse(S.Semigroup).concat('a', 'b'), console.log) // => 'ba'
문제. 위 reverse 는 유효한 combinator 이지만, 일반적으로 concat 연산은 교환법칙 을 만족하지 않습니다, 교환법칙을 만족하는 concat 과 그렇지 않은것을 찾을 수 있습니까?
Semigroup product
더 복잡한 semigroup 인스턴스를 정의해봅시다:
import * as N from 'fp-ts/number'
import { Semigroup } from 'fp-ts/Semigroup'
// 정점에서 시작하는 vector 를 모델링
type Vector = {
readonly x: number
readonly y: number
}
// 두 vector 의 합을 모델링
const SemigroupVector: Semigroup<Vector> = {
concat: (first, second) => ({
x: N.SemigroupSum.concat(first.x, second.x),
y: N.SemigroupSum.concat(first.y, second.y)
})
}
예제
const v1: Vector = { x: 1, y: 1 }
const v2: Vector = { x: 1, y: 2 }
console.log(SemigroupVector.concat(v1, v2)) // => { x: 2, y: 3 }
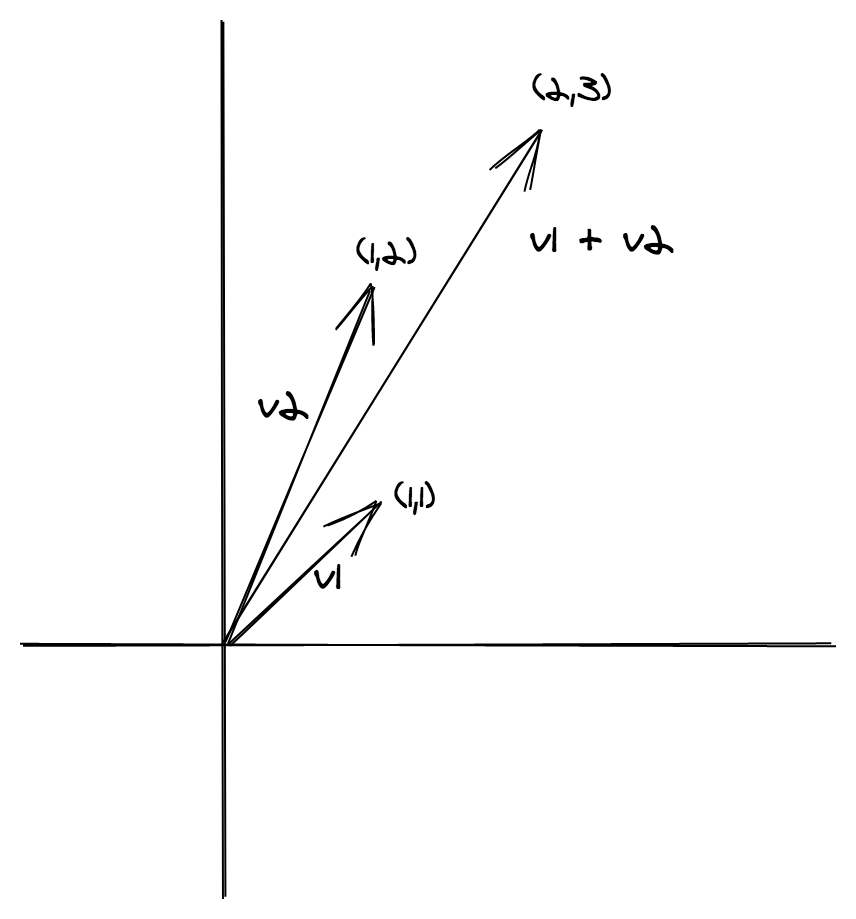
boilerplate 코드가 너무 많나요? 좋은 소식은 semigroup 의 수학적 법칙에 따르면 각 필드에 대한 semigroup 인스턴스를 만들 수 있다면 Vector 같은 구조체의 semigroup 인스턴스를 만들 수 있습니다.
편리하게도 fp-ts/Semigroup 모듈은 struct combinator 를 제공합니다:
import { struct } from 'fp-ts/Semigroup'
// 두 vector 의 합을 모델링
const SemigroupVector: Semigroup<Vector> = struct({
x: N.SemigroupSum,
y: N.SemigroupSum
})
참고. struct 와 유사한 tuple 에 대해 동작하는 combinator 도 존재합니다: tuple
import * as N from 'fp-ts/number'
import { Semigroup, tuple } from 'fp-ts/Semigroup'
// 정점에서 시작하는 vector 모델링
type Vector = readonly [number, number]
// 두 vector 의 합을 모델링
const SemigroupVector: Semigroup<Vector> = tuple(N.SemigroupSum, N.SemigroupSum)
const v1: Vector = [1, 1]
const v2: Vector = [1, 2]
console.log(SemigroupVector.concat(v1, v2)) // => [2, 3]
문제. 만약 임의의 Semigroup<A> 와 A 의 임의의 값 middle 을 두 concat 인자 사이에 넣도록 만든 인스턴스는 여전히 semigroup 일까요?
import { pipe } from 'fp-ts/function'
import { Semigroup } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'
export const intercalate = <A>(middle: A) => (
S: Semigroup<A>
): Semigroup<A> => ({
concat: (first, second) => S.concat(S.concat(first, middle), second)
})
const SemigroupIntercalate = pipe(S.Semigroup, intercalate('|'))
pipe(
SemigroupIntercalate.concat('a', SemigroupIntercalate.concat('b', 'c')),
console.log
) // => 'a|b|c'
임의의 타입에 대한 semigroup 인스턴스 찾기
결합법칙은 매우 까다로운 조건이기 때문에, 만약 어떤 타입 A 에 대한 결합법칙을 만족하는 연산을 찾을 수 없다면 어떻게될까요?
아래와 같은 User 를 정의했다고 가정합시다:
type User = {
readonly id: number
readonly name: string
}
그리고 데이터베이스에는 같은 User 에 대한 여러 복사본이 있다고 가정합니다 (예를들면 수정이력일 수 있습니다)
// 내부 API
declare const getCurrent: (id: number) => User
declare const getHistory: (id: number) => ReadonlyArray<User>
그리고 다음 외부 API 를 구현해야합니다.
export declare const getUser: (id: number) => User
API 는 다음 조건에 따라 적절한 User 를 가져와야 합니다. 조건은 가장 최근 또는 가장 오래된, 아니면 현재 값 등이 될 수 있습니다.
보통은 다음처럼 각 조건에 따라 여러 API 를 만들 수 있습니다:
export declare const getMostRecentUser: (id: number) => User
export declare const getLeastRecentUser: (id: number) => User
export declare const getCurrentUser: (id: number) => User
// etc...
따라서, User 를 반환하기 위해 모든 복사본에 대한 병합 (이나 선택)이 필요합니다. 이는 조건에 대한 문제를 Semigroup<User> 로 다룰 수 있다는 것을 의미합니다.
그렇지만, 아직 "두 User를 병합하기"가 어떤 의미인지, 그리고 해당 병합 연산이 결합법칙을 만족하는지 알기 쉽지 않습니다.
주어진 어떠한 타입 A 에 대해서도 항상 semigroup 인스턴스를 만들 수 있습니다. A 자체에 대한 인스턴스가 아닌 NonEmptyArray<A> 의 인스턴스로 만들 수 있으며 이는 A 의 free semigroup 이라고 불립니다.
import { Semigroup } from 'fp-ts/Semigroup'
// 적어도 하나의 A 의 요소가 있는 배열을 표현합니다
type ReadonlyNonEmptyArray<A> = ReadonlyArray<A> & {
readonly 0: A
}
// 비어있지 않은 두 배열을 합해도 여전히 비어있지 않은 배열입니다
const getSemigroup = <A>(): Semigroup<ReadonlyNonEmptyArray<A>> => ({
concat: (first, second) => [first[0], ...first.slice(1), ...second]
})
그러면 A 의 요소 ReadonlyNonEmptyArray<A> 의 "싱글톤" 으로 만들 수 있으며 이는 하나를 하나의 요소만 있는 배열을 의미합니다.
// 비어있지 않은 배열에 값 하나를 넣습니다
const of = <A>(a: A): ReadonlyNonEmptyArray<A> => [a]
이 방식을 User 타입에도 적용해봅시다:
import {
getSemigroup,
of,
ReadonlyNonEmptyArray
} from 'fp-ts/ReadonlyNonEmptyArray'
import { Semigroup } from 'fp-ts/Semigroup'
type User = {
readonly id: number
readonly name: string
}
// 이 semigroup 은 `User` 타입이 아닌 `ReadonlyNonEmptyArray<User>` 를 위한 것입니다
const S: Semigroup<ReadonlyNonEmptyArray<User>> = getSemigroup<User>()
declare const user1: User
declare const user2: User
declare const user3: User
// 병합: ReadonlyNonEmptyArray<User>
const merge = S.concat(S.concat(of(user1), of(user2)), of(user3))
// 배열에 직접 user 를 넣어서 같은 결과를 얻을 수 있습니다.
const merge2: ReadonlyNonEmptyArray<User> = [user1, user2, user3]
따라서, A 의 free semigroup 이란 비어있지 않은 모든 유한 순열을 다루는 semigroup 일 뿐입니다.
A 의 free semigroup 이란 데이터 내용을 유지한채로 A 의 요소들의 결합을 게으른 방법으로 처리하는 것으로 볼 수 있습니다.
이전 예제에서 [user1, user2, user3] 을 가지는 merge 상수는 어떤 요소가 어떤 순서로 결합되어 있는지 알려줍니다.
이제 getUser API 설계를 위한 세 가지 옵션이 있습니다:
Semigroup<User>를 정의하고 바로병합한다.
declare const SemigroupUser: Semigroup<User>
export const getUser = (id: number): User => {
const current = getCurrent(id)
const history = getHistory(id)
return concatAll(SemigroupUser)(current)(history)
}
Semigroup<User>을 직접 정의하는 대신 병합 전략을 외부에서 구현하게 한다. 즉 API 사용자가 제공하도록 한다.
export const getUser = (SemigroupUser: Semigroup<User>) => (
id: number
): User => {
const current = getCurrent(id)
const history = getHistory(id)
// 바로 병합
return concatAll(SemigroupUser)(current)(history)
}
Semigroup<User>를 정의할 수 없고 외부로 부터 제공받지 않는다.
이럴 때에는 User 의 free semigroup 을 활용합니다:
export const getUser = (id: number): ReadonlyNonEmptyArray<User> => {
const current = getCurrent(id)
const history = getHistory(id)
// 병합을 진행하지 않고 User 의 free semigroup 을 반환한다
return [current, ...history]
}
Semigroup<A> 인스턴스를 만들수 있는 상황일 지라도 다음과 같은 이유로 free semigroup 을 사용하는게 여전히 유용할 수 있습니다:
- 비싸고 무의미한 계산을 하지 않음
- semigroup 인스턴스를 직접 사용하지 않음
- API 사용자에게 (
concatAll을 사용해) 어떤 병합전략이 좋을지 결정할 수 있게함
Order-derivable Semigroups
만약 주어진 number 가 total order (전순서 집합, 어떤 임의의 x 와 y 를 선택해도, 다음 두 조건 중 하나가 참이다: x <= y 또는 y <= x) 라면 min 또는 max 연산을 활용해 또 다른 두 개의 Semigroup<number> 인스턴스를 얻을 수 있습니다.
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupMin: Semigroup<number> = {
concat: (first, second) => Math.min(first, second)
}
const SemigroupMax: Semigroup<number> = {
concat: (first, second) => Math.max(first, second)
}
문제. 왜 number 가 total order 이어야 할까요?
이러한 두 semigroup (SemigroupMin 과 SemigroupMax) 을 number 외 다른 타입에 대해서 정의한다면 유용할 것입니다.
다른 타입에 대해서도 전순서 집합 이라는 개념을 적용할 수 있을까요?
순서 의 개념을 설명하기 앞서 동등 의 개념을 생각할 필요가 있습니다.
Eq 를 활용한 동등성 모델링
이번에는 동등성의 개념을 모델링 해봅시다.
동치관계는 같은 유형의 요소의 동등이라는 개념을 의미합니다. 동치관계의 개념은 Typescript 의 interface 를 통해 구현할 수 있습니다.
interface Eq<A> {
readonly equals: (first: A, second: A) => boolean
}
직관적으로:
- 만약
equals(x, y) = true이면,x와y는 같다고 할 수 있습니다 - 만약
equals(x, y) = false이면,x와y는 다르다고 할 수 있습니다
예제
다음은 number 타입에 대한 Eq 인스턴스 입니다:
import { Eq } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
const EqNumber: Eq<number> = {
equals: (first, second) => first === second
}
pipe(EqNumber.equals(1, 1), console.log) // => true
pipe(EqNumber.equals(1, 2), console.log) // => false
인스턴스는 다음 법칙을 만족해야 합니다:
- 반사적:
A의 모든x에 대해equals(x, x) === true를 만족합니다 - 대칭적:
A의 모든x,y에 대해equals(x, y) === equals(y, x)를 만족합니다 - 전이적:
A의 모든x,y,z에 대해 만약equals(x, y) === true이고equals(y, z) === true이면,equals(x, z) === true를 만족합니다
문제. 다음 combinator 는 올바른 표현일까요? reverse: <A>(E: Eq<A>) => Eq<A>
문제. 다음 combinator 는 올바른 표현일까요? not: <A>(E: Eq<A>) => Eq<A>
import { Eq } from 'fp-ts/Eq'
export const not = <A>(E: Eq<A>): Eq<A> => ({
equals: (first, second) => !E.equals(first, second)
})
예제
주어진 요소가 ReadonlyArray 에 포함하는지 확인하는 elem 함수를 좀전에 만든 Eq 인스턴스를 사용해 구현해봅시다.
import { Eq } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
// 만약 `a` 가 `as` 리스트에 포함되면 `true` 를 반환합니다
const elem = <A>(E: Eq<A>) => (a: A) => (as: ReadonlyArray<A>): boolean =>
as.some((e) => E.equals(a, e))
pipe([1, 2, 3], elem(N.Eq)(2), console.log) // => true
pipe([1, 2, 3], elem(N.Eq)(4), console.log) // => false
왜 내장 includes 배열 메소드를 사용하지 않을까요?
console.log([1, 2, 3].includes(2)) // => true
console.log([1, 2, 3].includes(4)) // => false
Eq 인스턴스를 더 복잡한 타입에 대해 정의해봅시다.
import { Eq } from 'fp-ts/Eq'
type Point = {
readonly x: number
readonly y: number
}
const EqPoint: Eq<Point> = {
equals: (first, second) => first.x === second.x && first.y === second.y
}
console.log(EqPoint.equals({ x: 1, y: 2 }, { x: 1, y: 2 })) // => true
console.log(EqPoint.equals({ x: 1, y: 2 }, { x: 1, y: -2 })) // => false
그리고 elem 과 includes 의 결과를 확인해봅시다.
const points: ReadonlyArray<Point> = [
{ x: 0, y: 0 },
{ x: 1, y: 1 },
{ x: 2, y: 2 }
]
const search: Point = { x: 1, y: 1 }
console.log(points.includes(search)) // => false :(
console.log(pipe(points, elem(EqPoint)(search))) // => true :)
문제 (JavaScript). 왜 includes 메소드의 결과는 false 일까요?
사용자가 정의한 동등성 검사로직을 위한 유용한 API 가 없는 Javascript 같은 언어에서는 동등성의 개념을 추상화하는게 가장 중요합니다.
JavaScript 내장 Set 자료구조도 같은 이슈가 발생합니다:
type Point = {
readonly x: number
readonly y: number
}
const points: Set<Point> = new Set([{ x: 0, y: 0 }])
points.add({ x: 0, y: 0 })
console.log(points)
// => Set { { x: 0, y: 0 }, { x: 0, y: 0 } }
Set 은 값 비교를 위해 === ("엄격한 비교") 를 하기에, points 는 두개의 동일한 복사본인 { x: 0, y: 0 } 을 가지며 이는 우리는 원하는 결과가 아닙니다. 따라서 Set 에 요소를 추가하는 새로운 API 를 정의하는게 유용하며 그 방법 중 하나가 Eq 추상화를 활용하는 것입니다.
문제. 이 API 의 시그니쳐는 어떻게 될까요? 문제. What would be the signature of this API?
EqPoint 를 정의하는데 많은 boilerplate 코드가 필요할까요? 좋은 소식은 각각의 필드의 Eq 인스턴스를 정의할 수 있다면 Point 같은 구조체의 인스턴스도 정의할 수 있습니다.
fp-ts/Eq 모듈은 유용한 struct combinator 을 제공합니다:
import { Eq, struct } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
type Point = {
readonly x: number
readonly y: number
}
const EqPoint: Eq<Point> = struct({
x: N.Eq,
y: N.Eq
})
참고. Semigroup 처럼, 구조체 같은 데이터 타입에만 적용할 수 있는것은 아닙니다. tuple 에 적용되는 combinator 도 제공합니다: tuple
import { Eq, tuple } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
type Point = readonly [number, number]
const EqPoint: Eq<Point> = tuple(N.Eq, N.Eq)
console.log(EqPoint.equals([1, 2], [1, 2])) // => true
console.log(EqPoint.equals([1, 2], [1, -2])) // => false
fp-ts 에는 다른 combinator 들이 존재하며, 여기 ReadonlyArray 에 대한 Eq 인스턴스를 만들어주는 combinator 를 볼 수 있습니다.
import { Eq, tuple } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
import * as RA from 'fp-ts/ReadonlyArray'
type Point = readonly [number, number]
const EqPoint: Eq<Point> = tuple(N.Eq, N.Eq)
const EqPoints: Eq<ReadonlyArray<Point>> = RA.getEq(EqPoint)
Semigroups 처럼, 동일한 주어진 타입에 대한 하나 이상의 Eq 인스턴스를 만들 수 있습니다. 다음과 같은 User 모델이 있다고 가정해봅시다:
type User = {
readonly id: number
readonly name: string
}
struct combinator 를 활용해 "표준" Eq<User> 인스턴스를 만들 수 있습니다:
import { Eq, struct } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
import * as S from 'fp-ts/string'
type User = {
readonly id: number
readonly name: string
}
const EqStandard: Eq<User> = struct({
id: N.Eq,
name: S.Eq
})
Haskell 같은 더 순수한 함수형 언어에서는 데이터 타입에 따라 두개 이상의 Eq 인스턴스를 만드는 것을 허용하지 않습니다. 하지만 문맥에 따라 User 의 동등성의 의미가 달라질 수 있습니다. 흔한 예는 id 필드가 같다면 두 User 는 같다고 보는 것입니다.
/** `id` 필드가 동일하면 두 user 는 동일하다 */
const EqID: Eq<User> = {
equals: (first, second) => N.Eq.equals(first.id, second.id)
}
추상 개념을 구체적인 데이터 구조로 표현했으므로, 다른 일반적은 데이터 구조에 하듯 Eq 인스턴스를 프로그래밍적으로 다룰 수 있습니다. 예제를 살벼봅시다.
예제. 직접 EqId 을 정의하는 대신, contramap combinator 를 활용할 수 있습니다: Eq<A> 인스턴스와 B 에서 A 로 가는 함수가 주어지면, Eq<B> 를 만들 수 있습니다
import { Eq, struct, contramap } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import * as S from 'fp-ts/string'
type User = {
readonly id: number
readonly name: string
}
const EqStandard: Eq<User> = struct({
id: N.Eq,
name: S.Eq
})
const EqID: Eq<User> = pipe(
N.Eq,
contramap((user: User) => user.id)
)
console.log(
EqStandard.equals({ id: 1, name: 'Giulio' }, { id: 1, name: 'Giulio Canti' })
) // => false (`name` 필드가 다르기 때문에)
console.log(
EqID.equals({ id: 1, name: 'Giulio' }, { id: 1, name: 'Giulio Canti' })
) // => true (`name` 필드가 다를 지라도)
console.log(EqID.equals({ id: 1, name: 'Giulio' }, { id: 2, name: 'Giulio' }))
// => false (`name` 필드가 동일할 지라도)
문제. 주어진 데이터 타입 A 에 대해, Semigroup<Eq<A>> 을 정의할 수 있을까요? 정의할 수 있다면 무엇을 의미하는 걸까요?
Ord 를 활용한 순서 관계 모델링
이전 Eq 챕터에서 동등의 개념을 다루었습니다. 이번에는 순서에 대한 개념을 다루고자 합니다.
전순서 관계는 Typescript 로 다음과 같이 구현할 수 있습니다:
import { Eq } from 'fp-ts/lib/Eq'
type Ordering = -1 | 0 | 1
interface Ord<A> extends Eq<A> {
readonly compare: (x: A, y: A) => Ordering
}
결과적으로:
x < yif and only ifcompare(x, y) = -1x = yif and only ifcompare(x, y) = 0x > yif and only ifcompare(x, y) = 1
if and only if는 주어진 두 명제가 필요충분조건이라는 뜻입니다
Example
number 타입에 대한 Ord 인스턴스를 만들어봅시다:
import { Ord } from 'fp-ts/Ord'
const OrdNumber: Ord<number> = {
equals: (first, second) => first === second,
compare: (first, second) => (first < second ? -1 : first > second ? 1 : 0)
}
다음과 같은 조건을 만족합니다:
- 반사적:
A의 모든x에 대해compare(x, x) <= 0이다 - 반대칭적:
A의 모든x,y에 대해 만약compare(x, y) <= 0이고compare(y, x) <= 0이면x = y이다 - 추이적:
A의 모든x,y,z에 대해 만약compare(x, y) <= 0이고compare(y, z) <= 0이면compare(x, z) <= 0이다
Eq 의 equals 연산자는 compare 연산자와도 호환됩니다:
A 의 모든 x, y 에 대해 다음 두 명제는 필요충분조건입니다
compare(x, y) === 0 if and only if equals(x, y) === true
참고. equals 는 compare 를 활용해 다음 방법으로 도출할 수 있습니다:
equals: (first, second) => compare(first, second) === 0
사실 fp-ts/Ord 모듈에 있는 fromComapre 하는 경우 compare 함수만 제공하면 Ord 인스턴스를 만들어줍니다:
import { Ord, fromCompare } from 'fp-ts/Ord'
const OrdNumber: Ord<number> = fromCompare((first, second) =>
first < second ? -1 : first > second ? 1 : 0
)
문제. 가위바위보 게임에 대한 Ord 인스턴스를 정의할 수 있을까요? move1 <= move2 이면 move2 가 move1 를 이깁니다.
ReadonlyArray 요소의 정렬을 위한 sort 함수를 만들어보면서 Ord 인스턴스의 실용적인 사용법을 확인해봅시다.
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord } from 'fp-ts/Ord'
export const sort = <A>(O: Ord<A>) => (
as: ReadonlyArray<A>
): ReadonlyArray<A> => as.slice().sort(O.compare)
pipe([3, 1, 2], sort(N.Ord), console.log) // => [1, 2, 3]
문제 (JavaScript). 왜 sort 구현에서 내장 배열 메소드 slice 를 사용한걸까요?
주어진 두 값중 작은것을 반환하는 min 함수를 만들어보면서 또 다른 Ord 활용법을 살펴봅시다:
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord } from 'fp-ts/Ord'
const min = <A>(O: Ord<A>) => (second: A) => (first: A): A =>
O.compare(first, second) === 1 ? second : first
pipe(2, min(N.Ord)(1), console.log) // => 1
Dual Ordering
이전 챕터에서 concat 연산자를 반전시켜 dual semigroup 을 얻는 reverse combinator 를 만든것처럼, compare 연산자를 반전시켜 dual ordering 을 얻을 수 있습니다.
Ord 에 대한 reserve combinator 를 만들어봅시다:
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { fromCompare, Ord } from 'fp-ts/Ord'
export const reverse = <A>(O: Ord<A>): Ord<A> =>
fromCompare((first, second) => O.compare(second, first))
reverse 활용 예로 min 을 반전시켜 max 를 얻을 수 있습니다:
import { flow, pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord, reverse } from 'fp-ts/Ord'
const min = <A>(O: Ord<A>) => (second: A) => (first: A): A =>
O.compare(first, second) === 1 ? second : first
// const max: <A>(O: Ord<A>) => (second: A) => (first: A) => A
const max = flow(reverse, min)
pipe(2, max(N.Ord)(1), console.log) // => 2
전순서 (모든 x, y 에 대해 다음 조건이 만족합니다: x <= y 이거나 y <= z)는 숫자에 대해선 명백하게 만족하는 것으로 보이지만, 모든 상황에서 그런것은 아닙니다. 조금 더 복잡한 상황을 가정해봅시다:
type User = {
readonly name: string
readonly age: number
}
어떤 User 가 다른 User 보다 "작거나 같다"고 말하긴 어렵습니다.
어떻게 Ord<User> 인스턴스를 만들 수 있을까요?
문맥에 따라 다르지만, User 의 나이로 순서를 매기는 방법이 있습니다:
import * as N from 'fp-ts/number'
import { fromCompare, Ord } from 'fp-ts/Ord'
type User = {
readonly name: string
readonly age: number
}
const byAge: Ord<User> = fromCompare((first, second) =>
N.Ord.compare(first.age, second.age)
)
이번에도 contramap combinator 를 사용하면 Ord<A> 와 B 에서 A 로 가는 함수만 제공해 Ord<B> 를 만들 수 있으며 이를통해 작성하는 코드의 양을 줄일 수 있습니다:
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { contramap, Ord } from 'fp-ts/Ord'
type User = {
readonly name: string
readonly age: number
}
const byAge: Ord<User> = pipe(
N.Ord,
contramap((_: User) => _.age)
)
이전에 정의한 min 함수를 사용해 주어진 두 User 중 더 젊은 User 를 얻을 수 있습니다.
// const getYounger: (second: User) => (first: User) => User
const getYounger = min(byAge)
pipe(
{ name: 'Guido', age: 50 },
getYounger({ name: 'Giulio', age: 47 }),
console.log
) // => { name: 'Giulio', age: 47 }
문제. fp-ts/ReadonlyMap 모듈에는 다음과 같은 API 가 있습니다:
/**
* `ReadonlyMap` 의 키들이 정렬된 `ReadonlyArray` 를 얻습니다.
* Get a sorted `ReadonlyArray` of the keys contained in a `ReadonlyMap`.
*/
declare const keys: <K>(
O: Ord<K>
) => <A>(m: ReadonlyMap<K, A>) => ReadonlyArray<K>
왜 이 API 는 Ord<K> 인스턴스가 필요할까요?
이전에 만난 첫 문제상황으로 돌아가봅시다: number 가 아닌 다른 타입에 대한 다음 두 semigroup 을 정의하는 것입니다 SemigroupMin 과 SemigroupMax:
import { Semigroup } from 'fp-ts/Semigroup'
const SemigroupMin: Semigroup<number> = {
concat: (first, second) => Math.min(first, second)
}
const SemigroupMax: Semigroup<number> = {
concat: (first, second) => Math.max(first, second)
}
이제 Ord 추상화가 있기에 문제를 해결할 수 있습니다:
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { Ord, contramap } from 'fp-ts/Ord'
import { Semigroup } from 'fp-ts/Semigroup'
export const min = <A>(O: Ord<A>): Semigroup<A> => ({
concat: (first, second) => (O.compare(first, second) === 1 ? second : first)
})
export const max = <A>(O: Ord<A>): Semigroup<A> => ({
concat: (first, second) => (O.compare(first, second) === 1 ? first : second)
})
type User = {
readonly name: string
readonly age: number
}
const byAge: Ord<User> = pipe(
N.Ord,
contramap((_: User) => _.age)
)
console.log(
min(byAge).concat({ name: 'Guido', age: 50 }, { name: 'Giulio', age: 47 })
) // => { name: 'Giulio', age: 47 }
console.log(
max(byAge).concat({ name: 'Guido', age: 50 }, { name: 'Giulio', age: 47 })
) // => { name: 'Guido', age: 50 }
예제
다음 예제를 통해 지금까지 배운내용을 정리해봅시다 (Fantas, Eel, and Specification 4: Semigroup에서 차용함).
데이터베이스에 다음과 같은 형태의 고객의 기록이 있는 시스템을 구축하는 상황을 가정해봅시다:
interface Customer {
readonly name: string
readonly favouriteThings: ReadonlyArray<string>
readonly registeredAt: number // 유닉스 시간
readonly lastUpdatedAt: number // 유닉스 시간
readonly hasMadePurchase: boolean
}
어떤 이유에서인지, 같은 사람에 대한 중복 데이터가 존재할 수 있습니다.
병합 전략이 필요한 순간입니다. 하지만 우리에겐 Semigroup 있습니다!
import * as B from 'fp-ts/boolean'
import { pipe } from 'fp-ts/function'
import * as N from 'fp-ts/number'
import { contramap } from 'fp-ts/Ord'
import * as RA from 'fp-ts/ReadonlyArray'
import { max, min, Semigroup, struct } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'
interface Customer {
readonly name: string
readonly favouriteThings: ReadonlyArray<string>
readonly registeredAt: number // 유닉스 시간
readonly lastUpdatedAt: number // 유닉스 시간
readonly hasMadePurchase: boolean
}
const SemigroupCustomer: Semigroup<Customer> = struct({
// 더 긴 이름을 선택
name: max(pipe(N.Ord, contramap(S.size))),
// 모두 병합
favouriteThings: RA.getSemigroup<string>(),
// 가장 과거 일자를 선택
registeredAt: min(N.Ord),
// 가장 최근 일자를 선택
lastUpdatedAt: max(N.Ord),
// 논리합에 대한 boolean semigroup
hasMadePurchase: B.SemigroupAny
})
console.log(
SemigroupCustomer.concat(
{
name: 'Giulio',
favouriteThings: ['math', 'climbing'],
registeredAt: new Date(2018, 1, 20).getTime(),
lastUpdatedAt: new Date(2018, 2, 18).getTime(),
hasMadePurchase: false
},
{
name: 'Giulio Canti',
favouriteThings: ['functional programming'],
registeredAt: new Date(2018, 1, 22).getTime(),
lastUpdatedAt: new Date(2018, 2, 9).getTime(),
hasMadePurchase: true
}
)
)
/*
{ name: 'Giulio Canti',
favouriteThings: [ 'math', 'climbing', 'functional programming' ],
registeredAt: 1519081200000, // new Date(2018, 1, 20).getTime()
lastUpdatedAt: 1521327600000, // new Date(2018, 2, 18).getTime()
hasMadePurchase: true
}
*/
문제. 주어진 타입 A 에 대해 Semigroup<Ord<A>> 인스턴스를 만들 수 있나요? 가능하다면 무엇을 의미할까요?
Monoids 를 통한 합성 모델링
지금까지 배운것을 다시 정리해봅시다.
대수이 아래 조합으로 이루어져 있다는 것을 보았습니다:
- 타입
A - 타입
A와 연관된 몇가지 연산들 - 조합을 위한 몇가지 법칙과 속성
처음 살펴본 대수는 concat 으로 불리는 연산을 하나 가진 magma 였습니다. Magma<A> 에 대한 특별한 법칙은 없었고 다만 concat 연산이 A 에 대해 닫혀있어야 했습니다. 즉 다음 연산의 결과는
concat(first: A, second: A) => A
여전히 A 에 속해야 합니다.
이후 여기에 하나의 간단한 결합법칙 을 추가함으로써, Magma<A> 를 더 다듬어진 Semigroup<A> 을 얻게 되었습니다. 이를 통해 결합법칙이 병렬계산을 가능하게 해주는지 알게 되었습니다.
이제 Semigroup 에 또 다른 규칙을 추가하고자 합니다.
concat 연산이 있는 집합 A 에 대한 Semigorup 이 주어진 경우, 만약 집합 A 의 어떤 한 요소가 A 의 모든 요소 a 에 대해 다음 두 조건을 만족한다면 (이 요소를 empty 라 부르겠습니다)
- 우동등성(Right identity):
concat(a, empty) = a - 좌동등성(Left identity):
concat(empty, a) = a
이 Semigroup 은 또한 Moniod 입니다.
참고: 이후 내용에서는 empty 를 unit 으로 부르겠습니다. 다른 여러 동의어들이 있으며, 그 중 가장 많이 쓰이는 것은 neutral element 과 identity element 입니다.
import { Semigroup } from 'fp-ts/Semigroup'
interface Monoid<A> extends Semigroup<A> {
readonly empty: A
}
이전까지 본 많은 semigroup 들이 Monid 로 확장할 수 있었습니다. A 에 대해 우동등성과 좌동등성을 만족하는 요소를 찾기만 하면 됩니다.
import { Monoid } from 'fp-ts/Monoid'
/** 덧셈에 대한 number `Monoid` */
const MonoidSum: Monoid<number> = {
concat: (first, second) => first + second,
empty: 0
}
/** 곰셈에 대한 number `Monoid` */
const MonoidProduct: Monoid<number> = {
concat: (first, second) => first * second,
empty: 1
}
const MonoidString: Monoid<string> = {
concat: (first, second) => first + second,
empty: ''
}
/** 논리곱에 대한 boolean monoid */
const MonoidAll: Monoid<boolean> = {
concat: (first, second) => first && second,
empty: true
}
/** 논리합에 대한 boolean monoid */
const MonoidAny: Monoid<boolean> = {
concat: (first, second) => first || second,
empty: false
}
문제. 이전 섹션에서 타입 ReadonlyArray<string> 에 대한 Semigorup 인스턴스를 정의했습니다:
import { Semigroup } from 'fp-ts/Semigroup'
const Semigroup: Semigroup<ReadonlyArray<string>> = {
concat: (first, second) => first.concat(second)
}
이 semigroup 에 대한 unit 을 찾을 수 있을까요? 만약 그렇다면, ReadonlyArray<string> 뿐만 아니라 ReadonlyArray<A> 에 대해서도 그렇다고 일반화할 수 있을까요?
문제 (더 복잡함). 임의의 monoid 에 대해, unit 이 오직 하나만 있음을 증명해보세요.
위 증명을 통해 monoid 당 오직 하나의 unit 만 있다는 것이 보증되기에, 우리는 monoid 에서 unit 을 하나 찾았다면 더 이상 찾지 않아도 됩니다.
모든 semigroup 은 magma 이지만, 역은 성립하지 않았듯이, 모든 monoid 는 semigroup 이지만, 모든 semigroup 이 monoid 는 아닙니다.
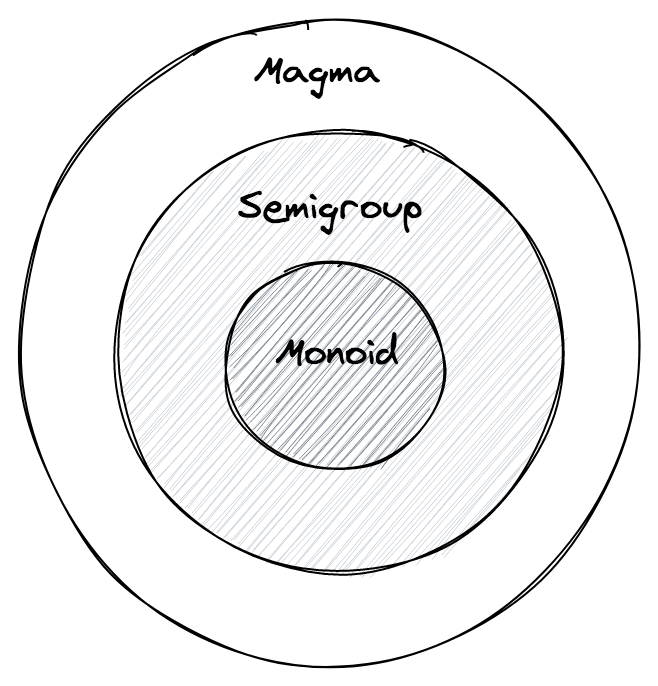
예제
다음 예제를 살펴봅시다:
import { pipe } from 'fp-ts/function'
import { intercalate } from 'fp-ts/Semigroup'
import * as S from 'fp-ts/string'
const SemigroupIntercalate = pipe(S.Semigroup, intercalate('|'))
console.log(S.Semigroup.concat('a', 'b')) // => 'ab'
console.log(SemigroupIntercalate.concat('a', 'b')) // => 'a|b'
console.log(SemigroupIntercalate.concat('a', '')) // => 'a|'
이 semigroup 은 concat(a, empty) = a 를 만족하는 string 타입인 empty 가 존재하지 않는점을 확인해주세요.
마지막으로, 함수가 포함된 더 "난해한" 예제입니다:
예제
endomorphism 은 입력과 출력 타입이 같은 함수를 말합니다:
type Endomorphism<A> = (a: A) => A
임의의 타입 A 에 대해, A 의 endomorphism 에 대해 다음과 같이 정의된 인스턴스는 monoid 입니다:
concat연산은 일반적인 함수 합성과 같습니다- unit 값은 항등함수 입니다
import { Endomorphism, flow, identity } from 'fp-ts/function'
import { Monoid } from 'fp-ts/Monoid'
export const getEndomorphismMonoid = <A>(): Monoid<Endomorphism<A>> => ({
concat: flow,
empty: identity
})
참고: identity 함수는 다음과 같은 구현 하나만 존재합니다:
const identity = (a: A) => a
입력으로 무엇을 받든지, 그것을 그대로 결과로 돌려줍니다.
concatAll 함수
semigroup 과 비교해서 monoid 의 한 가지 큰 특징은 다수의 요소를 결합하는게 훨씬 쉬워진다는 것입니다: 더 이상 초기값을 제공하지 않아도 됩니다.
import { concatAll } from 'fp-ts/Monoid'
import * as S from 'fp-ts/string'
import * as N from 'fp-ts/number'
import * as B from 'fp-ts/boolean'
console.log(concatAll(N.MonoidSum)([1, 2, 3, 4])) // => 10
console.log(concatAll(N.MonoidProduct)([1, 2, 3, 4])) // => 24
console.log(concatAll(S.Monoid)(['a', 'b', 'c'])) // => 'abc'
console.log(concatAll(B.MonoidAll)([true, false, true])) // => false
console.log(concatAll(B.MonoidAny)([true, false, true])) // => true
문제. 왜 초기값이 더 이상 필요없을까요?
Product monoid
이미 semigroup 에서 보았듯이, 각 필드에 대해 monoid 인스턴스를 정의할 수 있다면 구조체에 대한 monoid 인스턴스를 정의할 수 있습니다.
예제
import { Monoid, struct } from 'fp-ts/Monoid'
import * as N from 'fp-ts/number'
type Point = {
readonly x: number
readonly y: number
}
const Monoid: Monoid<Point> = struct({
x: N.MonoidSum,
y: N.MonoidSum
})
참고. struct 와 비슷하게 tuple 에 적용하는 combinator 가 있습니다: tuple.
import { Monoid, tuple } from 'fp-ts/Monoid'
import * as N from 'fp-ts/number'
type Point = readonly [number, number]
const Monoid: Monoid<Point> = tuple(N.MonoidSum, N.MonoidSum)
문제. 일반적인 타입 A 의 "free monoid" 를 정의할 수 있을까요?
데모 (캔버스에 기하학적 도형을 그리는 시스템 구현)
순수함수와 부분함수
첫 번째 챕터에서 순수함수에 대한 비공식적인 정의를 보았습니다:
순수함수란 같은 입력에 항상 같은 결과를 내는 관찰 가능한 부작용없는 절차입니다.
위와같은 비공식적 문구를 보고 다음과 같은 의문점이 생길 수 있습니다:
- "부작용"이란 무엇인가?
- "관찰가능하다"는 것은 무엇을 의미하는가?
- "같다"라는게 무엇을 의미하는가?
이 함수의 공식적인 정의를 살펴봅시다.
참고. 만약 X 와 Y 가 집합이면, X × Y 은 곱집합 이라 불리며 다음과 같은 집합을 의미합니다
X × Y = { (x, y) | x ∈ X, y ∈ Y }
다음 정의 는 한 세기 전에 만들어졌습니다:
정의. 함수 f: X ⟶ Y 는 X × Y 의 부분집합이면서 다음 조건을 만족합니다,
모든 x ∈ X 에 대해 (x, y) ∈ f 를 만족하는 오직 하나의 y ∈ Y 가 존재합니다.
집합 X 는 함수 f 의 정의역 이라 하며, Y 는 f 의 공역 이라 합니다.
예제
함수 double: Nat ⟶ Nat 곱집합 Nat × Nat 의 부분집합이며 형태는 다음과 같습니다: { (1, 2), (2, 4), (3, 6), ...}
Typescript 에서는 f 를 다음과 같이 정의할 수 있습니다
const f: Record<number, number> = {
1: 2,
2: 4,
3: 6
...
}
위 예제는 함수의 확장적 정의라고 불리며, 이는 정의역의 요소들을 꺼내 그것들 각각에 대해 공역의 원소에 대응하는 것을 의미합니다.
당연하게도, 이러한 집합이 무한이라면 문제가 발생한다는 것을 알 수 있습니다. 모든 함수의 정의역과 공역을 나열할 수 없기 때문입니다.
이 문제는 조건적 정의라고 불리는 것을 통해 해결할 수 있습니다. 예를들면 (x, y) ∈ f 인 모든 순서쌍에 대해 y = x * 2 가 만족한다는 조건을 표현하는 것입니다.
TypeScript 에서 다음과 같은 익숙한 형태인 double 함수의 정의를 볼 수 있습니다:
const double = (x: number): number => x * 2
곱집합의 부분집합으로서의 함수의 정의는 수작적으로 어떻게 모든 함수가 순수한지 보여줍니다: 어떠한 작용도, 상태 변경과 요소의 수정도 없습니다. 함수형 프로그래밍에서 함수의 구현은 가능한 한 이상적인 모델을 따라야합니다.
문제. 다음 절차(procedure) 중 순수 함수는 무엇일까요?
const coefficient1 = 2
export const f1 = (n: number) => n * coefficient1
// ------------------------------------------------------
let coefficient2 = 2
export const f2 = (n: number) => n * coefficient2++
// ------------------------------------------------------
let coefficient3 = 2
export const f3 = (n: number) => n * coefficient3
// ------------------------------------------------------
export const f4 = (n: number) => {
const out = n * 2
console.log(out)
return out
}
// ------------------------------------------------------
interface User {
readonly id: number
readonly name: string
}
export declare const f5: (id: number) => Promise<User>
// ------------------------------------------------------
import * as fs from 'fs'
export const f6 = (path: string): string =>
fs.readFileSync(path, { encoding: 'utf8' })
// ------------------------------------------------------
export const f7 = (
path: string,
callback: (err: Error | null, data: string) => void
): void => fs.readFile(path, { encoding: 'utf8' }, callback)
함수가 순수하다는 것이 꼭 지역변수의 변경 (local mutability)을 금지한다는 의미는 아닙니다. 변수가 함수 범위를 벗어나지 않는다면 변경할 수 있습니다.
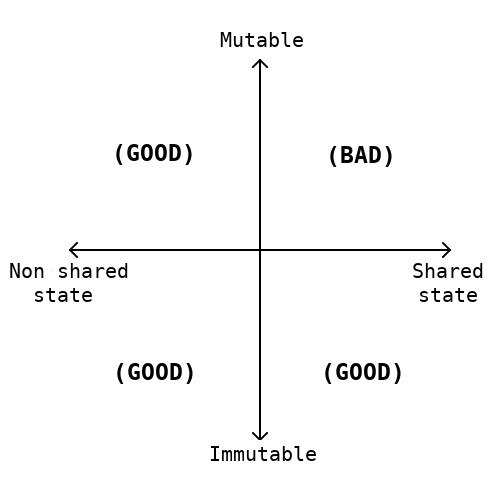
예제 (monoid 용 concatALl 함수 구현)
import { Monoid } from 'fp-ts/Monoid'
const concatAll = <A>(M: Monoid<A>) => (as: ReadonlyArray<A>): A => {
let out: A = M.empty // <= local mutability
for (const a of as) {
out = M.concat(out, a)
}
return out
}
궁극적인 목적은 참조 투명성 을 만족하는 것입니다.
우리의 API 사용자와의 계약은 API 의 signature 와 참조 투명성을 준수하겠다는 약속에 의해 정의됩니다.
declare const concatAll: <A>(M: Monoid<A>) => (as: ReadonlyArray<A>) => A
함수가 구현되는 방법에 대한 기술적 세부 사항은 관련이 없으므로, 구현 측면에서 많은 자유를 누릴 수 있습니다.
그렇다면, 우리는 부작용을 어떻게 정의해야 할까요? 단순히 참조 투명성 정의의 반대가 됩니다:
어떤 표현식이 참조 투명성을 지키지 않는다면 "부작용" 을 가지고 있습니다
함수는 함수형 프로그래밍의 두 가지 요소 중 하나인 참조 투명성의 완벽한 예시일 뿐만 아니라, 두 번째 요소한 합성 의 예시이기도 합니다.
함수 합성:
정의. 두 함수 f: Y ⟶ Z 와 g: X ⟶ Y 에 대해, 함수 h: X ⟶ Z 는 다음과 같이 정의된다:
h(x) = f(g(x))
이는 f 와 g 의 합성 이라하며 h = f ∘ g 라고 쓴다.
f 와 g 를 합성하려면, f 의 정의역이 g 의 공역에 포함되어야 한다는 점에 유의하시기 바랍니다.
정의. 정의역의 하나 이상의 값에 대해 정의되지 않는 함수는 부분함수 라고 합니다.
반대로, 정의역의 모든 원소에 대해 정의된 함수는 전체함수 라고 합니다.
예제
f(x) = 1 / x
함수 f: number ⟶ number 는 x = 0 에 대해서는 정의되지 않습니다.
예제
// `ReadonlyArray` 의 첫 번째 요소를 얻습니다
declare const head: <A>(as: ReadonlyArray<A>) => A
문제. 왜 head 는 부분함수 인가요?
문제. JSON.parse 는 전체함수 일까요?
parse: (text: string, reviver?: (this: any, key: string, value: any) => any) =>
any
문제. JSON.stringify 는 전체함수 일까요?
stringify: (
value: any,
replacer?: (this: any, key: string, value: any) => any,
space?: string | number
) => string
함수형 프로그래밍에서는 순수 및 전체함수 만 정의하는 경향이 있습니다. 지금부터 함수라는 용어는 "순수하면서 전체함수" 를 의미합니다. 그렇다면 애플리케이션에 부분함수가 있다면 어떻게 해야 할까요?
부분함수 f: X ⟶ Y 는 특별한 값(None 이라 부르겠습니다)을 공역에 더함으로써 언제나 전체함수로 되돌릴 수 있습니다.
정의되지 않은 모든 X 의 값을 None 에 대응하면 됩니다.
f': X ⟶ Y ∪ None
Y ∪ None 는 Option(Y) 와 동일하다고 정의한다면
f': X ⟶ Option(Y)
TypeScript 에서 Option 을 정의할 수 있을까요? 다음 장에서 그 방법을 살펴보겠습니다.
대수적 자료형
응용 프로그램이나 기능을 작성할 때 가장 좋은 첫 번째 단계는 도메인 모델을 정의하는 것입니다. TypeScript 는 이 작업을 수행하는 데 도움이 되는 많은 도구를 제공합니다. 대수적 자료형(줄여서 ADT)이 이러한 도구 중 하나입니다.
정의
컴퓨터 프로그래밍, 특히 함수형 프로그래밍과 타입 이론에서, 대수적 자료형은 복합 타입의 일종이다. 즉, 다른 타입을 조합하여 만든 타입이다.
대수적 자료형은 다음 두 개의 유형이 있습니다:
- 곱타입
- 합타입
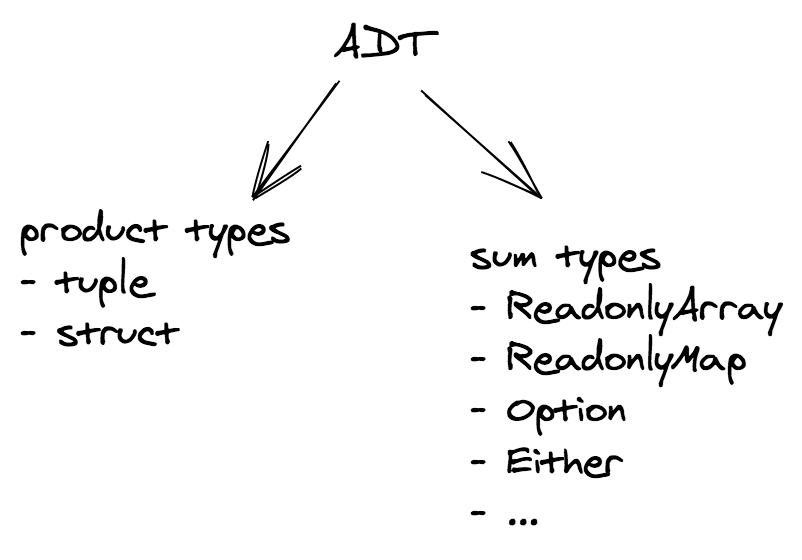
좀 더 친숙한 곱타입부터 시작해봅시다.
곱타입
곱타입은 집합 I 로 색인된 타입 Ti 의 목록입니다:
type Tuple1 = [string] // I = [0]
type Tuple2 = [string, number] // I = [0, 1]
type Tuple3 = [string, number, boolean] // I = [0, 1, 2]
// Accessing by index
type Fst = Tuple2[0] // string
type Snd = Tuple2[1] // number
구조체의 경우, I 는 label 의 집합입니다:
// I = {"name", "age"}
interface Person {
name: string
age: number
}
// label 을 통한 접근
type Name = Person['name'] // string
type Age = Person['age'] // number
곱타입은 다형적(polymorphic) 일 수 있습니다.
예제
// ↓ 타입 파라미터
type HttpResponse<A> = {
readonly code: number
readonly body: A
}
왜 "곱"타입 이라 하는가?
만약 A 의 요소의 개수를 C(A) 로 표기한다면 (수학에서는 cardinality 로 부릅니다), 다음 방적식은 참입니다:
C([A, B]) = C(A) * C(B)
곱의 cardinality 는 각 cardinality 들의 곱과 같습니다
예제
null 타입의 cardinality 는 1 입니다. 왜냐하면 null 하나의 요소만 가지기 때문입니다.
문제: boolean 타입의 cardinality 는 어떻게 될까요?
예제
type Hour = 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12
type Period = 'AM' | 'PM'
type Clock = [Hour, Period]
Hour 타입은 12 개의 요소를 가지고 있습니다. has 12 members.
Period 타입은 2 개의 요소를 가지고 있습니다. has 2 members.
따라서 Clock 타입은 12 * 2 = 24 개의 요소를 가지고 있습니다.
문제: 다음 Clock 타입의 cardinality 는 무엇일까요?
// 이전과 같음
type Hour = 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12
// 이전과 같음
type Period = 'AM' | 'PM'
// 형태만 다름, tuple 타입이 아님
type Clock = {
readonly hour: Hour
readonly period: Period
}
언제 곱타입을 쓸 수 있나요?
각 구성 요소가 독립적 이면 사용할 수 있습니다.
type Clock = [Hour, Period]
여기서 Hour 와 Period 는 독립적입니다: Hour 값이 Period 의 값을 바꾸지 않습니다. 모든 가능한 쌍 [Hour, Period] 는 이치 에 맞고 올바릅니다.
합타입
합타입은 서로 다른 (하지만 제한적인) 유형의 값을 가질 수 있는 자료형입니다. 하나의 인스턴스는 이 유형 중 오직 하나에 속하며 보통 이들 유형을 구분하기 위한 "tag" 값이 존재합니다.
TypeScript 공식 문서에는 이들을 discriminated union 으로 부릅니다.
이 union 의 각 멤버들은 disjoint(서로소) 이어야 하며, 어떤 값이 두 개 이상의 멤버에 속할 수 없습니다.
예제
type StringsOrNumbers = ReadonlyArray<string> | ReadonlyArray<number>
declare const sn: StringsOrNumbers
sn.map() // error: This expression is not callable.
위 타입은 두 멤버가 빈 배열을 의미하는 [] 를 포함하기 때문에 서로소가 아닙니다.
문제. 다음 조합은 서로소인가요?
type Member1 = { readonly a: string }
type Member2 = { readonly b: number }
type MyUnion = Member1 | Member2
서로소 조합은 함수형 프로그래밍에서 재귀적입니다.
다행히 TypeScript 는 조합이 서로소임을 보장할 수 있는 방법이 있습니다: tag 로 동작하는 필드를 추가하는 것입니다.
참고: 서로소 조합, 합타입 그리고 태그된 조합은 같은 의미로 사용됩니다.
예제 (redux actions)
Action 합타입은 사용자가 todo app 에서 수행할 수 있는 작업의 일부를 모델링합니다.
type Action =
| {
type: 'ADD_TODO'
text: string
}
| {
type: 'UPDATE_TODO'
id: number
text: string
completed: boolean
}
| {
type: 'DELETE_TODO'
id: number
}
type 태그가 각 멤버가 서로소임을 보장하게 해줍니다.
참고. 태그역할을 하는 필드이름은 개발자가 선택하는 것입니다. 꼭 "type" 일 필요는 없습니다. fp-ts 에서는, 보통 _tag 필드를 사용합니다.
몇 개의 예제를 보았으니 이제 대수적 자료형을 보다 명확하게 정의할 수 있습니다:
일반적으로, 대수적 자료형은 하나 이상의 독립적 요소들의 합이며, 여기서 각 요소는 0개 이상의 필드의 곱으로 이루어져 있다.
합타입은 다형적이고 재귀적일 수 있습니다.
예제 (연결 리스트)
// ↓ 타입 파라미터
export type List<A> =
| { readonly _tag: 'Nil' }
| { readonly _tag: 'Cons'; readonly head: A; readonly tail: List<A> }
// ↑ 재귀
문제 (TypeScript). 다음 자료형들은 곱타입 인가요? 합타입 인가요?
ReadonlyArray<A>Record<string, A>Record<'k1' | 'k2', A>ReadonlyMap<string, A>ReadonlyMap<'k1' | 'k2', A>
생성자
n 개의 요소를 가진 합타입은 각 멤버에 대해 하나씩 최소 n 개의 생성자 가 필요합니다:
예제 (redux action creators)
export type Action =
| {
readonly type: 'ADD_TODO'
readonly text: string
}
| {
readonly type: 'UPDATE_TODO'
readonly id: number
readonly text: string
readonly completed: boolean
}
| {
readonly type: 'DELETE_TODO'
readonly id: number
}
export const add = (text: string): Action => ({
type: 'ADD_TODO',
text
})
export const update = (
id: number,
text: string,
completed: boolean
): Action => ({
type: 'UPDATE_TODO',
id,
text,
completed
})
export const del = (id: number): Action => ({
type: 'DELETE_TODO',
id
})
예제 (TypeScript, 연결 리스트)
export type List<A> =
| { readonly _tag: 'Nil' }
| { readonly _tag: 'Cons'; readonly head: A; readonly tail: List<A> }
// null 생성자는 상수로 구현할 수 있습니다
export const nil: List<never> = { _tag: 'Nil' }
export const cons = <A>(head: A, tail: List<A>): List<A> => ({
_tag: 'Cons',
head,
tail
})
// 다음 배열과 동일합니다 [1, 2, 3]
const myList = cons(1, cons(2, cons(3, nil)))
Pattern matching
JavaScript 는 pattern matching 을 지원하지 않습니다 (TypeScript 도 마찬가지입니다) 하지만 match 함수로 시뮬레이션 할 수 있습니다.
예제 (TypeScript, 연결 리스트)
interface Nil {
readonly _tag: 'Nil'
}
interface Cons<A> {
readonly _tag: 'Cons'
readonly head: A
readonly tail: List<A>
}
export type List<A> = Nil | Cons<A>
export const match = <R, A>(
onNil: () => R,
onCons: (head: A, tail: List<A>) => R
) => (fa: List<A>): R => {
switch (fa._tag) {
case 'Nil':
return onNil()
case 'Cons':
return onCons(fa.head, fa.tail)
}
}
// 리스트가 비어있다면 `true` 를 반환합니다
export const isEmpty = match(
() => true,
() => false
)
// 리스트의 첫 번째 요소를 반환하거나 없다면 `undefined` 를 반환합니다
export const head = match(
() => undefined,
(head, _tail) => head
)
// 재귀적으로, 리스트의 길이를 계산해 반환합니다
export const length: <A>(fa: List<A>) => number = match(
() => 0,
(_, tail) => 1 + length(tail)
)
문제. head 가 최적의 API 가 아닌 이유는 무엇일까요?
참고. TypeScript 는 합타입에 대한 유용한 기능을 제공합니다: exhaustive check. Type checker 는 함수 본문에 정의된 switch 가 모든 경우에 대해 처리하고 있는지 검증 할 수 있습니다.
왜 "합"타입 이라 하는가?
왜냐하면 다음 항등식이 성립하기 때문입니다:
C(A | B) = C(A) + C(B)
합의 cardinality 는 각 cardinality 들의 합과 같습니다
예제 (Option 타입)
interface None {
readonly _tag: 'None'
}
interface Some<A> {
readonly _tag: 'Some'
readonly value: A
}
type Option<A> = None | Some<A>
일반적인 공식인 C(Option<A>) = 1 + C(A) 를 통해, Option<boolean> 의 cardinality 를 계산할 수 있습니다: 1 + 2 = 3 개의 멤버를 가집니다.
언제 합타입을 써야하나요?
곱타입으로 구현된 각 요소가 의존적 일 때입니다.
Example (React props)
import * as React from 'react'
interface Props {
readonly editable: boolean
readonly onChange?: (text: string) => void
}
class Textbox extends React.Component<Props> {
render() {
if (this.props.editable) {
// 오류: onChange 가 'undefined' 일 수 있어서 호출할 수 없습니다 :(
this.props.onChange('a')
}
return <div />
}
}
문제는 Props 가 곱타입으로 모델링되었지만, onChange 는 editable 에 의존 하는 것입니다.
이 경우에는 합타입이 더 유용합니다:
import * as React from 'react'
type Props =
| {
readonly type: 'READONLY'
}
| {
readonly type: 'EDITABLE'
readonly onChange: (text: string) => void
}
class Textbox extends React.Component<Props> {
render() {
switch (this.props.type) {
case 'EDITABLE':
this.props.onChange('a') // :)
}
return <div />
}
}
예제 (node callbacks)
declare function readFile(
path: string,
// ↓ ---------- ↓ CallbackArgs
callback: (err?: Error, data?: string) => void
): void
readFile 의 연산 결과는 callback 함수를 통해 전달되는 곱타입처럼 모델링됩니다 (정확히 말하면, tuple):
type CallbackArgs = [Error | undefined, string | undefined]
callback 요소들은 서로 의존적 입니다: Error 를 얻거나 또는 string 를 얻습니다:
| err | data | legal? |
|---|---|---|
Error | undefined | ✓ |
undefined | string | ✓ |
Error | string | ✘ |
undefined | undefined | ✘ |
이 API 는 다음과 같은 전제하에 모델링되지 않았습니다:
불가능한 상태를 나타낼 수 없게합니다
합타입이 더 좋은 선택입니다만, 어떤 합타입을 써야할까요? 이후 오류를 함수적인 방법으로 처리하는 방법을 다룰것입니다.
문제. 최근 callback 기반 API 들은 상당 부분 Promise 로 대체되고 있습니다.
declare function readFile(path: string): Promise<string>
TypeScript 같은 정적 타입 언어에서 Promise 를 사용할 때의 단점을 찾을 수 있나요?
함수적 오류 처리
오류를 어떻게 함수적으로 다루는지 알아봅시다.
오류를 반환하거나 던지는 함수는 부분 함수의 예입니다.
이전 챕터에서 모든 부분 함수 f 는 전체 함수인 f 로 만들 수 있음을 보았습니다.
f': X ⟶ Option(Y)
이제 TypeScript 에서의 합타입에 대해 알고 있으니 큰 문제없이 Option 을 정의할 수 있습니다.
Option 타입
Option 타입은 실패하거나 (None 의 경우) A 타입을 반환하는 (Some 의 경우) 계산의 효과를 표현합니다.
// 실패를 표현합니다
interface None {
readonly _tag: 'None'
}
// 성공을 표현합니다
interface Some<A> {
readonly _tag: 'Some'
readonly value: A
}
type Option<A> = None | Some<A>
생성자와 패턴 매칭은 다음과 같습니다:
const none: Option<never> = { _tag: 'None' }
const some = <A>(value: A): Option<A> => ({ _tag: 'Some', value })
const match = <R, A>(onNone: () => R, onSome: (a: A) => R) => (
fa: Option<A>
): R => {
switch (fa._tag) {
case 'None':
return onNone()
case 'Some':
return onSome(fa.value)
}
}
Option 타입은 오류를 던지는 것을 방지하거나 선택적인 값을 표현하는데 사용할 수 있습니다, 따라서 다음과 같은 코드를 개선할 수 있습니다:
// 거짓말 입니다 ↓
const head = <A>(as: ReadonlyArray<A>): A => {
if (as.length === 0) {
throw new Error('Empty array')
}
return as[0]
}
let s: string
try {
s = String(head([]))
} catch (e) {
s = e.message
}
위 타입 시스템은 실패의 가능성을 무시하고 있습니다.
import { pipe } from 'fp-ts/function'
// ↓ 타입 시스템은 계산이 실패할 수 있음을 "표현"합니다
const head = <A>(as: ReadonlyArray<A>): Option<A> =>
as.length === 0 ? none : some(as[0])
declare const numbers: ReadonlyArray<number>
const result = pipe(
head(numbers),
match(
() => 'Empty array',
(n) => String(n)
)
)
위 예제는 에러 발생 가능성이 타입 시스템에 들어있습니다.
만약 Option 의 value 값을 검증없이 접근하는 경우, 타입 시스템이 오류의 가능성을 알려줍니다:
declare const numbers: ReadonlyArray<number>
const result = head(numbers)
result.value // type checker 오류: 'value' 프로퍼티가 'Option<number>' 에 존재하지 않습니다
Option 에 들어있는 값을 접근할 수 있는 유일한 방법은 match 함수를 사용해 실패 상황도 같이 처리하는 것입니다.
pipe(result, match(
() => ...오류 처리...
(n) => ...이후 비즈니스 로직을 처리합니다...
))
이전 챕터에서 보았던 추상화에 대한 인스턴스틀 정의할 수 있을까요? Eq 부터 시작해봅시다.
Eq 인스턴스
두 개의 Option<string> 타입을 가지고 있고 두 값이 동일한지 확인하고 싶다고 해봅시다:
import { pipe } from 'fp-ts/function'
import { match, Option } from 'fp-ts/Option'
declare const o1: Option<string>
declare const o2: Option<string>
const result: boolean = pipe(
o1,
match(
// o1 이 none 인 경우
() =>
pipe(
o2,
match(
// o2 가 none 인 경우
() => true,
// o2 가 some 인 경우
() => false
)
),
// o1 이 some 인 경우
(s1) =>
pipe(
o2,
match(
// o2 가 none 인 경우
() => false,
// o2 가 some 인 경우
(s2) => s1 === s2 // 여기서 엄격한 동등을 사용합니다
)
)
)
)
만약 두 개의 Option<number> 가 있다면 어떻게 될까요? 아마 위와 비슷한 코드를 또 작성하는건 번거로울 것입니다. 결국 차이가 발생하는 부분은 Option 에 포함된 두 값을 비교하는 방법이라 할 수 있습니다.
따라서 사용자에게 A 에 대한 Eq 인스턴스를 받아 Option<A> 에 대한 Eq 인스턴스를 만드는 방법으로 일반화 할 수 있습니다.
다른 말로 하자면 우리는 getEq combinator 를 정의할 수 있습니다: 임의의 Eq<A> 를 받아 Eq<Option<A>> 를 반환합니다:
import { Eq } from 'fp-ts/Eq'
import { pipe } from 'fp-ts/function'
import { match, Option, none, some } from 'fp-ts/Option'
export const getEq = <A>(E: Eq<A>): Eq<Option<A>> => ({
equals: (first, second) =>
pipe(
first,
match(
() =>
pipe(
second,
match(
() => true,
() => false
)
),
(a1) =>
pipe(
second,
match(
() => false,
(a2) => E.equals(a1, a2) // 여기서 `A` 를 비교합니다
)
)
)
)
})
import * as S from 'fp-ts/string'
const EqOptionString = getEq(S.Eq)
console.log(EqOptionString.equals(none, none)) // => true
console.log(EqOptionString.equals(none, some('b'))) // => false
console.log(EqOptionString.equals(some('a'), none)) // => false
console.log(EqOptionString.equals(some('a'), some('b'))) // => false
console.log(EqOptionString.equals(some('a'), some('a'))) // => true
Option<A> 타입에 대한 Eq 인스턴스를 정의함으로 얻게되는 가장 좋은 점은 이전에 보았던 Eq 에 대한 모든 조합에 대해 응용할 수 있다는 점입니다.
(원문) The best thing about being able to define an
Eqinstance for a typeOption<A>is being able to leverage all of the combiners we've seen previously forEq.
예제:
Option<readonly [string, number]> 타입에 대한 Eq 인스턴스:
import { tuple } from 'fp-ts/Eq'
import * as N from 'fp-ts/number'
import { getEq, Option, some } from 'fp-ts/Option'
import * as S from 'fp-ts/string'
type MyTuple = readonly [string, number]
const EqMyTuple = tuple<MyTuple>(S.Eq, N.Eq)
const EqOptionMyTuple = getEq(EqMyTuple)
const o1: Option<MyTuple> = some(['a', 1])
const o2: Option<MyTuple> = some(['a', 2])
const o3: Option<MyTuple> = some(['b', 1])
console.log(EqOptionMyTuple.equals(o1, o1)) // => true
console.log(EqOptionMyTuple.equals(o1, o2)) // => false
console.log(EqOptionMyTuple.equals(o1, o3)) // => false
위 코드에서 import 부분만 살짝 바꾸면 Ord 에 대한 비슷한 결과를 얻을 수 있습니다:
import * as N from 'fp-ts/number'
import { getOrd, Option, some } from 'fp-ts/Option'
import { tuple } from 'fp-ts/Ord'
import * as S from 'fp-ts/string'
type MyTuple = readonly [string, number]
const OrdMyTuple = tuple<MyTuple>(S.Ord, N.Ord)
const OrdOptionMyTuple = getOrd(OrdMyTuple)
const o1: Option<MyTuple> = some(['a', 1])
const o2: Option<MyTuple> = some(['a', 2])
const o3: Option<MyTuple> = some(['b', 1])
console.log(OrdOptionMyTuple.compare(o1, o1)) // => 0
console.log(OrdOptionMyTuple.compare(o1, o2)) // => -1
console.log(OrdOptionMyTuple.compare(o1, o3)) // => -1
Semigroup, Monoid 인스턴스
이제, 두 개의 다른 Option<A> 를 "병합" 한다고 가정합시다: 다음과 같은 네 가지 경우가 있습니다:
| x | y | concat(x, y) |
|---|---|---|
| none | none | none |
| some(a) | none | none |
| none | some(a) | none |
| some(a) | some(b) | ? |
마지막 조건에서 문제가 발생합니다. 두 개의 A 를 "병합" 하는 방법이 필요합니다.
그런 방법이 있다면 좋을텐데... 그러고보니 우리의 옛 친구 Semigroup 이 하는 일 아닌가요?
| x | y | concat(x, y) |
|---|---|---|
| some(a1) | some(a2) | some(S.concat(a1, a2)) |
이제 우리가 할 일은 사용자로부터 A 에 대한 Semigroup 을 받고 Option<A> 에 대한 Semigroup 인스턴스를 만드는 것입니다.
// 구현은 연습문제로 남겨두겠습니다
declare const getApplySemigroup: <A>(S: Semigroup<A>) => Semigroup<Option<A>>
문제. 위 semigroup 을 monoid 로 만들기 위한 항등원을 추가할 수 있을까요?
// 구현은 연습문제로 남겨두겠습니다
declare const getApplicativeMonoid: <A>(M: Monoid<A>) => Monoid<Option<A>>
다음과 같이 동작하는 Option<A> 의 monoid 인스턴스를 정의할 수 있습니다:
| x | y | concat(x, y) |
|---|---|---|
| none | none | none |
| some(a1) | none | some(a1) |
| none | some(a2) | some(a2) |
| some(a1) | some(a2) | some(S.concat(a1, a2)) |
// 구현은 연습문제로 남겨두겠습니다
declare const getMonoid: <A>(S: Semigroup<A>) => Monoid<Option<A>>
문제. 이 monoid 의 empty 멤버는 무엇일까요?
예제
getMonoid 를 사용해 다음 두 개의 유용한 monoid 을 얻을 수 있습니다:
(가장 왼쪽에 있는 None 이 아닌 값을 반환하는 Monoid)
| x | y | concat(x, y) |
|---|---|---|
| none | none | none |
| some(a1) | none | some(a1) |
| none | some(a2) | some(a2) |
| some(a1) | some(a2) | some(a1) |
import { Monoid } from 'fp-ts/Monoid'
import { getMonoid, Option } from 'fp-ts/Option'
import { first } from 'fp-ts/Semigroup'
export const getFirstMonoid = <A = never>(): Monoid<Option<A>> =>
getMonoid(first())
(가장 오른쪽에 있는 None 이 아닌 값을 반환하는 Monoid)
| x | y | concat(x, y) |
|---|---|---|
| none | none | none |
| some(a1) | none | some(a1) |
| none | some(a2) | some(a2) |
| some(a1) | some(a2) | some(a2) |
import { Monoid } from 'fp-ts/Monoid'
import { getMonoid, Option } from 'fp-ts/Option'
import { last } from 'fp-ts/Semigroup'
export const getLastMonoid = <A = never>(): Monoid<Option<A>> =>
getMonoid(last())
Example
getLastMonoid 는 선택적인 값을 관리하는데 유용합니다. 다음 VSCode 텍스트 편집기의 사용자 설정을 알아내는 예제를 살펴봅시다.
import { Monoid, struct } from 'fp-ts/Monoid'
import { getMonoid, none, Option, some } from 'fp-ts/Option'
import { last } from 'fp-ts/Semigroup'
/** VSCode 설정 */
interface Settings {
/** 글꼴 조정 */
readonly fontFamily: Option<string>
/** 픽셀 단위의 글꼴 크기 조정 */
readonly fontSize: Option<number>
/** 일정 개수의 열로 표현하기 위해 minimap 의 길이를 제한 */
readonly maxColumn: Option<number>
}
const monoidSettings: Monoid<Settings> = struct({
fontFamily: getMonoid(last()),
fontSize: getMonoid(last()),
maxColumn: getMonoid(last())
})
const workspaceSettings: Settings = {
fontFamily: some('Courier'),
fontSize: none,
maxColumn: some(80)
}
const userSettings: Settings = {
fontFamily: some('Fira Code'),
fontSize: some(12),
maxColumn: none
}
/** userSettings 은 workspaceSettings 을 덮어씌웁니다 */
console.log(monoidSettings.concat(workspaceSettings, userSettings))
/*
{ fontFamily: some("Fira Code"),
fontSize: some(12),
maxColumn: some(80) }
*/
문제. 만약 VSCode 가 한 줄당 80 개 이상의 열을 관리할 수 없다고 가정해봅시다. 그렇다면 monoidSettings 을 어떻게 수정하면 이 제한사항을 반영할 수 있을까요?
Either 타입
계산의 실패나 오류를 던지는 부분 함수를 다루기 위해 어떻게 Option 자료형을 활용하는지 살펴보았습니다.
하미잔 이 자료형은 어떤 상황에서는 제한적일 수 있습니다. 성공하는 경우 A 의 정보를 포함한 Some<A> 을 얻지만 None 은 어떠한 데이터도 가지고 있지 않습니다. 즉 실패했다는 것은 알지만 그 이유를 알 수 없습니다.
이를 해결하기 위해 실패를 표현하는 새로운 자료형이 필요하며 이를 Left<E> 로 부르겠습니다. 또한 Some<A> 도 Right<A> 로 변경됩니다.
// 실패를 표현
interface Left<E> {
readonly _tag: 'Left'
readonly left: E
}
// 성공을 표현
interface Right<A> {
readonly _tag: 'Right'
readonly right: A
}
type Either<E, A> = Left<E> | Right<A>
생성자와 패턴 매칭은 다음과 같습니다:
const left = <E, A>(left: E): Either<E, A> => ({ _tag: 'Left', left })
const right = <A, E>(right: A): Either<E, A> => ({ _tag: 'Right', right })
const match = <E, R, A>(onLeft: (left: E) => R, onRight: (right: A) => R) => (
fa: Either<E, A>
): R => {
switch (fa._tag) {
case 'Left':
return onLeft(fa.left)
case 'Right':
return onRight(fa.right)
}
}
이전 callback 예제로 돌아가봅시다:
declare function readFile(
path: string,
callback: (err?: Error, data?: string) => void
): void
readFile('./myfile', (err, data) => {
let message: string
if (err !== undefined) {
message = `Error: ${err.message}`
} else if (data !== undefined) {
message = `Data: ${data.trim()}`
} else {
// should never happen
message = 'The impossible happened'
}
console.log(message)
})
이제 다음과 같이 signature 를 변경할 수 있습니다:
declare function readFile(
path: string,
callback: (result: Either<Error, string>) => void
): void
그리고 다음과 같이 사용합니다:
readFile('./myfile', (e) =>
pipe(
e,
match(
(err) => `Error: ${err.message}`,
(data) => `Data: ${data.trim()}`
),
console.log
)
)
Category theory
지금까지 함수형 프로그래밍의 기초인 합성 에 대해 살펴보았습니다.
문제를 어떻게 해결하나요? 우리는 큰 문제를 작은 문제로 분할합니다. 만약 작은 문제들이 여전히 크다면, 더 작게 분할합니다. 마지막으로, 작은 문제들을 해결하는 코드를 작성합니다. 그리고 여기서 프로그래밍의 정수가 등장합니다: 우리는 큰 문제를 해결하기 위해 작은 문제를 다시 합성합니다. 만약 조각을 다시 되돌릴 수 없다면 분할은 아무 의미도 없을 것입니다. - Bartosz Milewski
이 말은 정확히 무엇을 의미하는 걸까요? 어떻게 두 조각이 합성 되는지 알 수 있을까요? 두 조각이 잘 합성된다는 것은 어떤 의미일까요?
만약 결합된 엔티티를 변경하지 않고 각각의 행동을 쉽고 일반적으로 결합할 수 있다면 엔티티들은 합성가능하다고 말한다. 나는 재사용성과 프로그래밍 모델에서 간결하게 표현되는 조합적 확장을 달성하기 위한 이루기 위해 가장 중요한 요소가 합성가능성 이라고 생각한다. - Paul Chiusano
함수형 스타일로 작성된 프로그램이 파이프라인과 얼마나 유사한지 간략하게 언급하였습니다:
const program = pipe(
input,
f1, // 순수 함수
f2, // 순수 함수
f3, // 순수 함수
...
)
하지만 이런 스타일로 코딩하는 것은 얼마나 간단한 걸까요? 한번 시도해봅시다:
import { pipe } from 'fp-ts/function'
import * as RA from 'fp-ts/ReadonlyArray'
const double = (n: number): number => n * 2
/**
* 프로그램은 주어진 ReadonlyArray<number> 의 첫 번째 요소를 두 배한 값을 반환합니다
*/
const program = (input: ReadonlyArray<number>): number =>
pipe(
input,
RA.head, // 컴파일 에러! 타입 'Option<number>' 는 'number' 에 할당할 수 없습니다
double
)
왜 컴파일 에러가 발생할까요? 왜냐하면 head 와 double 을 합성할 수 없기 때문입니다.
head: (as: ReadonlyArray<number>) => Option<number>
double: (n: number) => number
head 의 공역은 double 의 정의역에 포함되지 않습니다.
순수함수로 프로그램을 만드려는 우리의 시도는 끝난걸까요?
우리는 그러한 근본적인 질문에 답할 수 있는 엄격한 이론 을 찾아야 합니다.
우리는 합성가능성에 대한 공식적인 정의 가 필요합니다.
다행히도, 지난 70년 동안, 가장 오래되고 가장 큰 인류의 오픈 소스 프로젝트 (수학) 의 구성원과 많은 수의 연구원들이 합성가능성에 대한 다음 이론을 개발하는데 몰두했습니다. category theory, Saunders Mac Lane along Samuel Eilenberg (1945) 에 의해 시작된 수학의 한 분야.
category 는 합성의 본질이라 할 수 있습니다.


다음 장에서 어떻게 category 가 다음 기반을 구성할 수 있는지 살펴볼 것입니다:
- 일반적인 프로그래밍 언어 를 위한 모델
- 합성 의 개념을 위한 모델
정의
category 의 정의는 그렇게 복잡하진 않지만, 조금 길기 때문에 두 부분으로 나누겠습니다:
- 첫 번째는 단지 기술적인 것입니다 (구성요소를 정의할 필요가 있습니다)
- 두 번째는 우리가 관심있는 합성에 더 연관되어 있습니다
첫 번째 (구성요소)
category 는 (Objects, Morphisms) 쌍으로 되어있고 각각 다음을 의미합니다:
Objects는 object 들의 목록입니다Morphisms는 object 들 간의 morphisms 의 목록 ("arrow" 라고도 불립니다) 입니다
참고. "object" 라는 용어는 프로그래밍에서의 "객체" 와는 관련이 없습니다. 단지 "object" 를 확인할 수 없는 블랙박스나, 다양한 morphisms 을 정의하는데 유용한 단순한 placeholder 라고 생각해주세요.
모든 morphisms f 는 원천 object A 와 대상 object B 를 가지고 있습니다.
모든 morphism 에서, A 와 B 는 모두 Ojbects 의 구성원입니다. 보통 f: A ⟼ B 라고 쓰며 "f 는 A 에서 B 로 가는 morphism" 이라 말합니다.
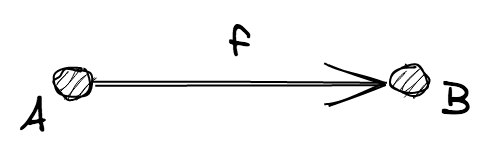
참고. 앞으로는, 단순하게 원은 제외하고 object 에만 라벨을 붙이겠습니다>
두 번째 (합성)
다음 속성을 만족하는 "합성" 이라 불리는 ∘ 연산이 존재합니다:
- (morphisms 의 합성) 모든 임의의 두 morphisms
f: A ⟼ B와g: B ⟼ C에 대해f와g의 합성 인 다음g ∘ f: A ⟼ Cmorphism 이 존재해야 합니다.
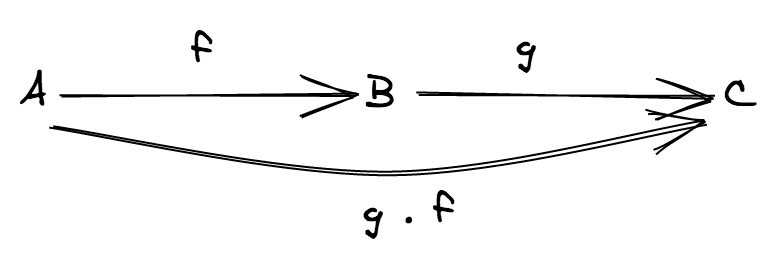
- (결합 법칙) 만약
f: A ⟼ B,g: B ⟼ C이고h: C ⟼ D이면h ∘ (g ∘ f) = (h ∘ g) ∘ f
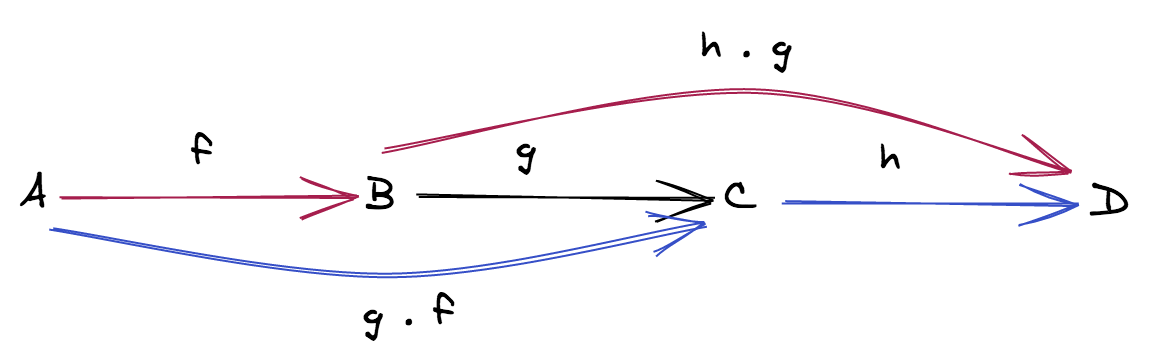
- (항등성) 모든
X의 object 에 대해, 다음 법칙을 만족하는 identity morphism 이라 불리는 morphismidentity: X ⟼ X가 존재합니다. 모든 임의의 morphismf: A ⟼ X와g: X ⟼ B에 대해,identity ∘ f = f와g ∘ identity = g식을 만족합니다.
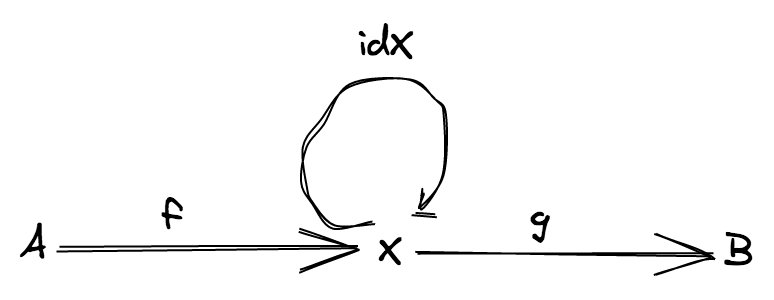
예제
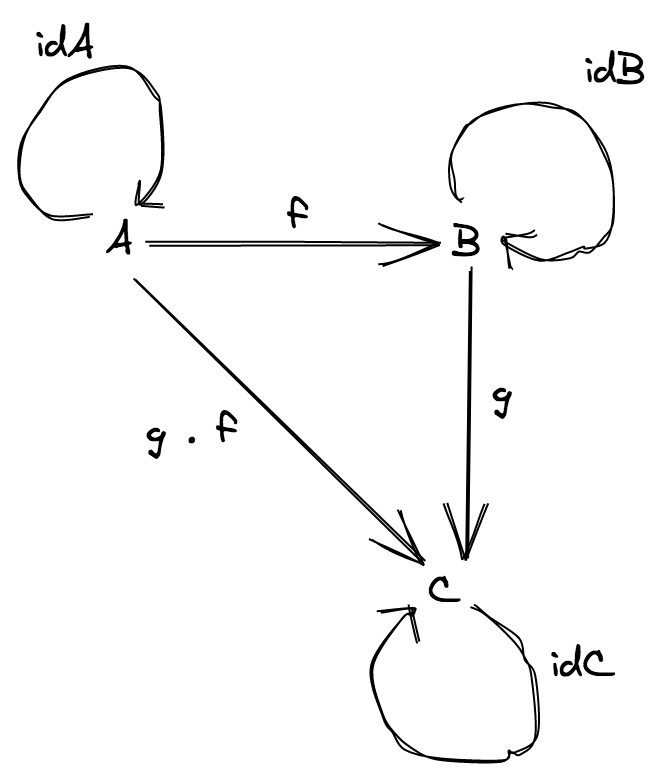
category 는 매우 단순합니다, 3 개의 objects 와 6 개의 morphism 이 존재합니다 (1A, 1B, 1C 와 A, B, C 에 대한 identity morphism 들 입니다).
Category 로 프로그래밍 언어 모델링
Category 는 타입이 있는 프로그래밍 언어 의 단순화된 모델로 볼 수 있습니다.
- object 는 타입 으로
- morphism 은 함수 로
∘을 일반적인 함수의 합성 으로
다음 다이어그램에서:

3가지 타입과 6가지 함수를 가진 가상의 (그리고 단순한) 프로그래밍 언어로 생각할 수 있습니다.
예를 들면:
A = stringB = numberC = booleanf = string => numberg = number => booleang ∘ f = string => boolean
그리고 다음과 같이 구현할 수 있습니다:
const idA = (s: string): string => s
const idB = (n: number): string => n
const idC = (b: boolean): boolean => b
const f = (s: string): number => s.length
const g = (n: number): boolean => n > 2
// gf = g ∘ f
const gf = (s: string): boolean => g(f(s))
Category 로 구현한 TypeScript
TypeScript 언어를 단순화한 TS 라고 불리는 category 를 정의해봅시다:
- object 는 TypeScript 의 타입입니다:
string,number,ReadonlyArray<string>, 등... - morphism 은 TypeScript 함수입니다:
(a: A) => B,(b: B) => C, ... 여기서A,B,C, ... 는 TypeScript 의 타입 - identity morphism 은 단일 다형 함수를 의미합니다
const identity = <A>(a: A): A => a - morphism 의 합성 은 (결합법칙을 만족하는) 일반적인 함수의 합성입니다
TypeScript 모델 TS category 는 다소 제한적으로 보일 수 있습니다: 반목문도 없고, if 문도 없으며, 대부분 기능이 없습니다... 하지만 잘 정의된 합성의 개념을 활용하면 이 모델은 우리가 목표에 도달하는 데 도움이 될 만큼 충분히 풍부하다고 할 수 있습니다.
(원문) As a model of TypeScript, the TS category may seem a bit limited: no loops, no
ifs, there's almost nothing... that being said that simplified model is rich enough to help us reach our goal: to reason about a well-defined notion of composition.
합성의 핵심 문제
TS category 에서 다음 두 개의 일반적인 함수를 합성할 수 있습니다. f: (a: A) => B 와 g: (c: C) => D, 여기서 C = B
function flow<A, B, C>(f: (a: A) => B, g: (b: B) => C): (a: A) => C {
return (a) => g(f(a))
}
function pipe<A, B, C>(a: A, f: (a: A) => B, g: (b: B) => C): C {
return flow(f, g)(a)
}
하지만 B != C 인 경우에는 어떻게 될까요? 어떻게 그러한 두 함수를 합성할 수 있을까요? 포기해야 할까요?
다음 장에서, 어떠한 조건에서 두 함수의 합성이 가능한지 살펴보겠습니다.
스포일러
f: (a: A) => B와g: (b: B) => C의 합성은 일반적인 함수의 합성을 사용합니다 we use our usual function compositionf: (a: A) => F<B>와g: (b: B) => C의 합성은F의 functor 인스턴스가 필요합니다f: (a: A) => F<B>와g: (b: B, c: C) => D의 합성은F의 applicative functor 인스턴스가 필요합니다f: (a: A) => F<B>와g: (b: B) => F<C>의 합성은F의 monad 인스턴스가 필요합니다
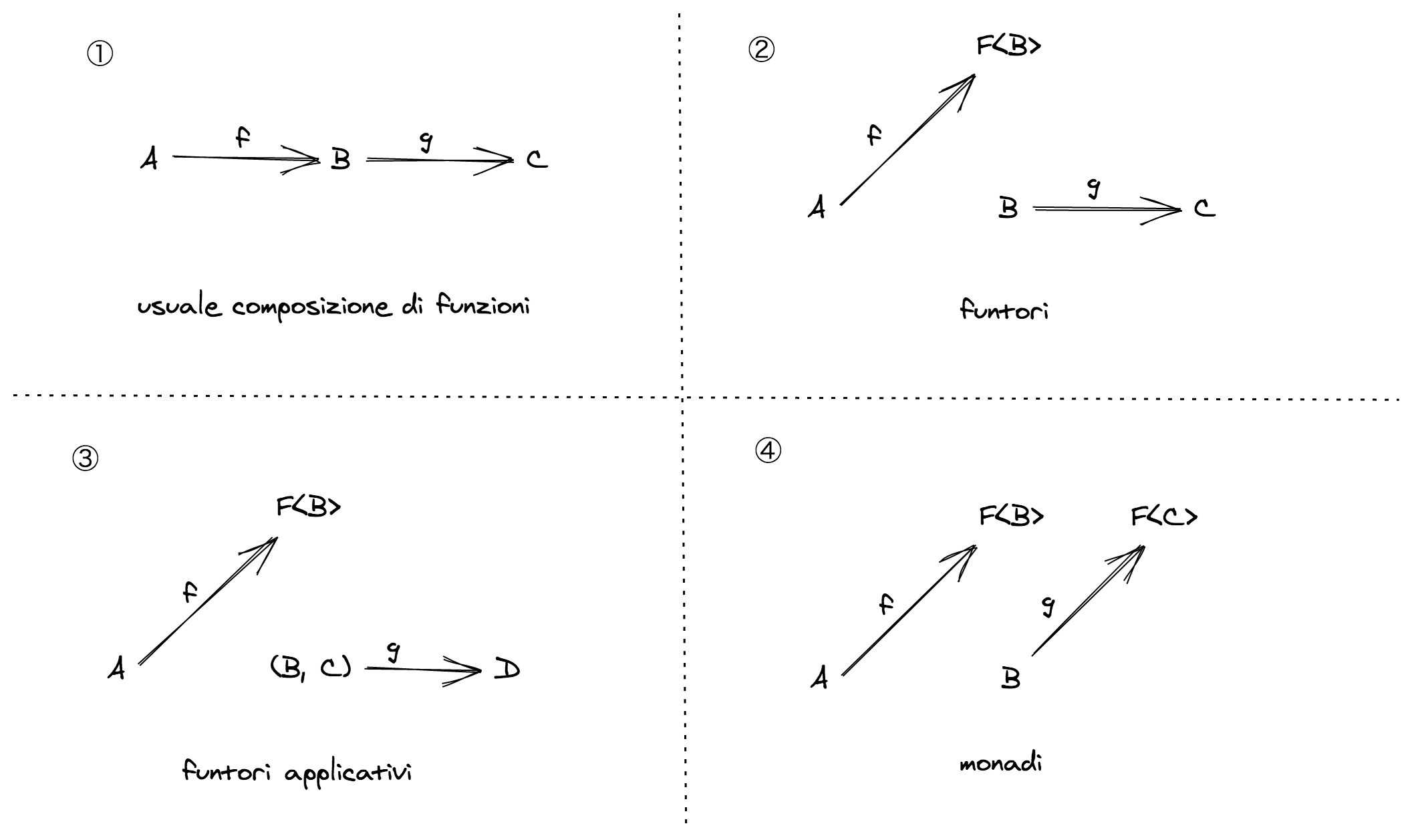
이번 장의 초반에 언급한 문제가 두 번째 상황에 해당하며 F 는 Option 타입을 의미합니다:
// A = ReadonlyArray<number>, B = number, F = Option
head: (as: ReadonlyArray<number>) => Option<number>
double: (n: number) => number
문제를 해결하기 위해, 다음 장에서 functor 에 대해 알아봅시다.
Functors
이전 섹션에서 TS category (TypeScript category) 와 함수 합성의 핵심 문제에 대해 살펴보았습니다:
어떻게 두 일반적인 함수
f: (a: A) => B와g: (c: C) => D를 합성할 수 있을까요?
왜 이 문제의 해결법을 찾는게 그렇게 중요할까요?
왜냐하면, 만약 category 로 프로그래밍 언어를 모델링하는데 사용할 수 있다면, morphism (TS category 에서 함수) 을 활용해 프로그램 을 모델링할 수 있기 때문입니다.
따라서, 이 추상적인 문제를 푸는 것은 일반적인 방법으로 프로그램을 합성 하는 구체적인 방법을 찾는 것을 의미합니다. 그리고 이것은 우리 개발자들에게 정말 흥미로운 일입니다, 그렇지 않나요?
프로그램으로서의 함수
만약 함수로 프로그램을 모델링하고 싶다면 다음과 같은 문제를 해결해야합니다:
어떻게 순수함수로 부작용을 발생시키는 프로그램을 모델링 할 수 있는가?
정답은 효과 (effects) 를 통해 부작용을 모델링하는 것인데, 이는 부작용을 표현 하는 수단으로 생각할 수 있습니다.
JavaScript 에서 가능한 두 가지 기법을 살펴보겠습니다:
- 효과를 위한 DSL (domain specific language) 을 정의
- thunk 를 사용
DSL 을 사용하는 첫 번째 방법은 다음과 같은 프로그램을
function log(message: string): void {
console.log(message) // 부작용
}
아래와 부작용에 대한 설명 을 반환하는 함수로 수정해 공역을 변경하는 것입니다:
type DSL = ... // 시스템이 처리할 수 있는 모든 effect 의 합타입
function log(message: string): DSL {
return {
type: "log",
message
}
}
문제. 새롭게 정의한 log 함수는 정말로 순수한가요? log('foo') !== log('foo') 임을 유의해주세요!
이 기법은 effect 와 최종 프로그램을 시작할 때 부작용을 실행할 수 있는 인터프리터의 정의를 결합하는 방법이 필요합니다.
TypeScript 에서는 더 간단한 방법인 두 번째 기법은, 계산작업을 thunk 로 감싸는 것입니다:
// 비동기적인 부작용을 의미하는 thunk
type IO<A> = () => A
const log = (message: string): IO<void> => {
return () => console.log(message) // thunk 를 반환합니다
}
log 함수는 호출 시에는 부작용을 발생시키진 않지만, (action 이라 불리는) 계산작업을 나타내는 값 을 반환합니다.
import { IO } from 'fp-ts/IO'
export const log = (message: string): IO<void> => {
return () => console.log(message) // thunk 를 반환합니다
}
export const main = log('hello!')
// 이 시점에서는 로그를 출력하지 않습니다
// 왜냐하면 `main` 은 단지 계산작업을 나타내는 비활성 값이기 때문입니다.
main()
// 프로그램을 실행시킬 때 결과를 확인할 수 있습니다
함수형 프로그래밍에서는 (effect 의 형태를 가진) 부작용을 (main 함수로 불리는) 시스템의 경계에 밀어넣는 경향이 있습니다. 즉 시스템은 다음과 같은 형태를 가지며 인터프리터에 의해 실행됩니다.
system = pure core + imperative shell
(Haskell, PureScript 또는 Elm 과 같은) 순수 함수형 언어들은 언어 자체가 위 내용을 엄격하고 명확하게 지킬것을 요구합니다.
(원문) In purely functional languages (like Haskell, PureScript or Elm) this division is strict and clear and imposed by the very languages.
(fp-ts 에서 사용된) 이 thunk 기법또한 effect 를 결합할 수 있는 방법이 필요한데, 이는 일반적인 방법으로 프로그램을 합성하는 법을 찾아야 함을 의미합니다.
그 전에 우선 (비공식적인) 용어가 필요합니다: 다음 시그니쳐를 가진 함수를 순수 프로그램 이라 합시다:
(a: A) => B
이러한 시그니처는 A 타입의 입력을 받아 B 타입의 결과를 아무런 effect 없이 반환하는 프로그램을 의미합니다.
예제
len 프로그램:
const len = (s: string): number => s.length
이제 다음 시그니쳐를 가진 함수를 effectful 프로그램 이라 합시다:
(a: A) => F<B>
이러한 시그니쳐는 A 타입의 입력을 받아 B 타입과 effect F 를 함께 반환하는 프로그램을 의미합니다. 여기서 F 는 일종의 type constructor 입니다.
type constructor 는 n 개의 타입 연산자로 하나 이상의 타입을 받아 또 다른 타입을 반환합니다. 이전에 본 Option, ReadonlyArray, Either 와 같은 것이 type constructor 에 해당합니다.
예제
head 프로그램:
import { Option, some, none } from 'fp-ts/Option'
const head = <A>(as: ReadonlyArray<A>): Option<A> =>
as.length === 0 ? none : some(as[0])
이 프로그램은 Option effect 를 가집니다.
effect 를 다루다보면 다음과 같은 n 개의 타입을 받는 type constructor 를 살펴봐야 합니다.
| Type constructor | Effect (interpretation) |
|---|---|
ReadonlyArray<A> | 비 결정적 계산작업 |
Option<A> | 실패할 수 있는 계산작업 |
Either<E, A> | 실패할 수 있는 계산작업 |
IO<A> | 절대 실패하지 않는 동기 계산작업 |
Task<A> | 절대 실패하지 않는 비동기 계잔작업 |
Reader<R, A> | 외부 환경의 값 읽기 |
여기서
// `Promise` 를 반환하는 thunk
type Task<A> = () => Promise<A>
// `R` 은 계산에 필요한 "environment" 를 의미합니다
// 그 값을 읽을 수 있으며 `A` 를 결과로 반환합니다
type Reader<R, A> = (r: R) => A
이전의 핵심 문제로 돌아가봅시다:
어떻게 두 일반적인 함수
f: (a: A) => B와g: (c: C) => D를 합성할 수 있을까요?
지금까지 알아본 규칙으로는 이 일반적인 문제를 해결할 수 없습니다. 우리는 B 와 C 에 약간의 경계 를 추가해야 합니다.
B = C 의 경우에는 일반적인 함수 합성으로 해결할 수 있음을 알고 있습니다.
function flow<A, B, C>(f: (a: A) => B, g: (b: B) => C): (a: A) => C {
return (a) => g(f(a))
}
하지만 다른 경우에는 어떻게 해야할까요?
Functor 로 이어지는 경계
어떤 type constructor F 에 대해 B = F<C> 를 만족한다고 가정합시다. 그리고 다음과 같은 상황에서:
f: (a: A) => F<B>는 effectful 프로그램 입니다g: (b: B) => C는 순수함수 입니다
f 와 g 를 합성하기 위해서 (b: B) => C 인 g 함수를 일반적인 함수 합성을 사용할 수 있는 형태인 (fb: F<B>) => F<C> 로 만드는 과정이 필요합니다. (이러면 f 의 공역은 새로운 함수의 정의역과 일치하게 됩니다)
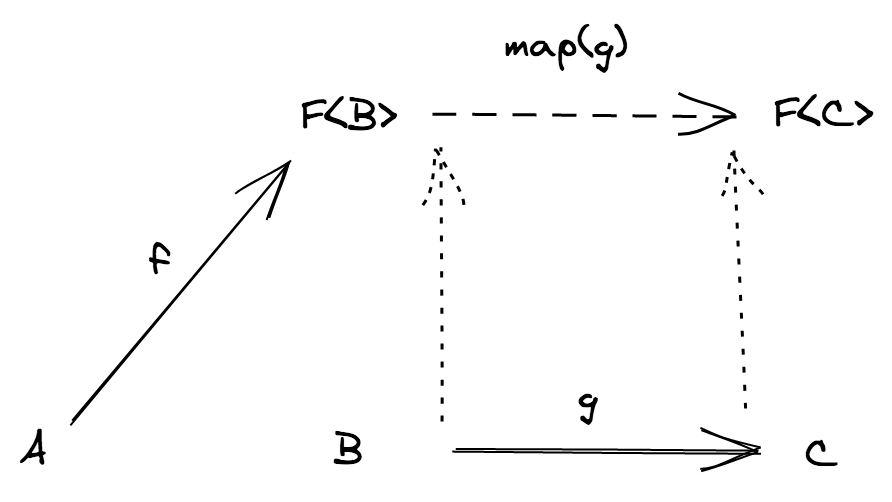
이제 기존 문제를 다음의 새로운 문제로 변경하였습니다: 위 방식을 위한, map 이라고 불리는 함수를 찾을 수 있을까요?
실용적인 예제를 살펴봅시다:
예제 (F = ReadonlyArray)
import { flow, pipe } from 'fp-ts/function'
// 함수 `B -> C` 를 `ReadonlyArray<B> -> ReadonlyArray<C>` 로 변형합니다
const map = <B, C>(g: (b: B) => C) => (
fb: ReadonlyArray<B>
): ReadonlyArray<C> => fb.map(g)
// -------------------
// 사용 예제
// -------------------
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const getFollowers = (user: User): ReadonlyArray<User> => user.followers
const getName = (user: User): string => user.name
// getFollowersNames: User -> ReadonlyArray<string>
const getFollowersNames = flow(getFollowers, map(getName))
// `flow` 대신 `pipe` 를 사용해봅시다...
export const getFollowersNames2 = (user: User) =>
pipe(user, getFollowers, map(getName))
const user: User = {
id: 1,
name: 'Ruth R. Gonzalez',
followers: [
{ id: 2, name: 'Terry R. Emerson', followers: [] },
{ id: 3, name: 'Marsha J. Joslyn', followers: [] }
]
}
console.log(getFollowersNames(user)) // => [ 'Terry R. Emerson', 'Marsha J. Joslyn' ]
예제 (F = Option)
import { flow } from 'fp-ts/function'
import { none, Option, match, some } from 'fp-ts/Option'
// 함수 `B -> C` 를 `Option<B> -> Option<C>` 로 변형합니다
const map = <B, C>(g: (b: B) => C): ((fb: Option<B>) => Option<C>) =>
match(
() => none,
(b) => {
const c = g(b)
return some(c)
}
)
// -------------------
// 사용 예제
// -------------------
import * as RA from 'fp-ts/ReadonlyArray'
const head: (input: ReadonlyArray<number>) => Option<number> = RA.head
const double = (n: number): number => n * 2
// getDoubleHead: ReadonlyArray<number> -> Option<number>
const getDoubleHead = flow(head, map(double))
console.log(getDoubleHead([1, 2, 3])) // => some(2)
console.log(getDoubleHead([])) // => none
예제 (F = IO)
import { flow } from 'fp-ts/function'
import { IO } from 'fp-ts/IO'
// 함수 `B -> C` 를 `IO<B> -> IO<C>` 로 변형합니다
const map = <B, C>(g: (b: B) => C) => (fb: IO<B>): IO<C> => () => {
const b = fb()
return g(b)
}
// -------------------
// 사용 예제
// -------------------
interface User {
readonly id: number
readonly name: string
}
// 더미 인메모리 데이터베이스
const database: Record<number, User> = {
1: { id: 1, name: 'Ruth R. Gonzalez' },
2: { id: 2, name: 'Terry R. Emerson' },
3: { id: 3, name: 'Marsha J. Joslyn' }
}
const getUser = (id: number): IO<User> => () => database[id]
const getName = (user: User): string => user.name
// getUserName: number -> IO<string>
const getUserName = flow(getUser, map(getName))
console.log(getUserName(1)()) // => Ruth R. Gonzalez
예제 (F = Task)
import { flow } from 'fp-ts/function'
import { Task } from 'fp-ts/Task'
// 함수 `B -> C` 를 `Task<B> -> Task<C>` 로 변형합니다
const map = <B, C>(g: (b: B) => C) => (fb: Task<B>): Task<C> => () => {
const promise = fb()
return promise.then(g)
}
// -------------------
// 사용 예제
// -------------------
interface User {
readonly id: number
readonly name: string
}
// 더미 원격 데이터베이스
const database: Record<number, User> = {
1: { id: 1, name: 'Ruth R. Gonzalez' },
2: { id: 2, name: 'Terry R. Emerson' },
3: { id: 3, name: 'Marsha J. Joslyn' }
}
const getUser = (id: number): Task<User> => () => Promise.resolve(database[id])
const getName = (user: User): string => user.name
// getUserName: number -> Task<string>
const getUserName = flow(getUser, map(getName))
getUserName(1)().then(console.log) // => Ruth R. Gonzalez
예제 (F = Reader)
import { flow } from 'fp-ts/function'
import { Reader } from 'fp-ts/Reader'
// 함수 `B -> C` 를 `Reader<R, B> -> Reader<R, C>` 로 변형합니다
const map = <B, C>(g: (b: B) => C) => <R>(fb: Reader<R, B>): Reader<R, C> => (
r
) => {
const b = fb(r)
return g(b)
}
// -------------------
// 사용 예제
// -------------------
interface User {
readonly id: number
readonly name: string
}
interface Env {
// 더미 인메모리 데이터베이스
readonly database: Record<string, User>
}
const getUser = (id: number): Reader<Env, User> => (env) => env.database[id]
const getName = (user: User): string => user.name
// getUserName: number -> Reader<Env, string>
const getUserName = flow(getUser, map(getName))
console.log(
getUserName(1)({
database: {
1: { id: 1, name: 'Ruth R. Gonzalez' },
2: { id: 2, name: 'Terry R. Emerson' },
3: { id: 3, name: 'Marsha J. Joslyn' }
}
})
) // => Ruth R. Gonzalez
더 일반적으로, type constructor F 가 map 함수를 가질때, 이를 functor 인스턴스 라고 합니다.
(원문) More generally, when a type constructor
Fadmits amapfunction, we say it admits a functor instance.
수학적인 관점에서는, functor 는 category 의 구조를 유지하는 category 간의 map 이라 할 수 있으며, 이는 identity morphisms 과 합성 연산을 그대로 유지하게 만들어줍니다.
category 는 object 와 morphism 의 쌍이기에, functor 또한 두 개의 쌍입니다:
- C 의 모든 object
X를 object D 로 묶는 object 간의 매핑. - C 의 모든 morphism
f를 D 의 morphismmap(f)로 묶는 morphism 간의 매핑.
여기서 C 와 D 는 (프로그래밍 언어라고 할 수 있는) category 입니다.
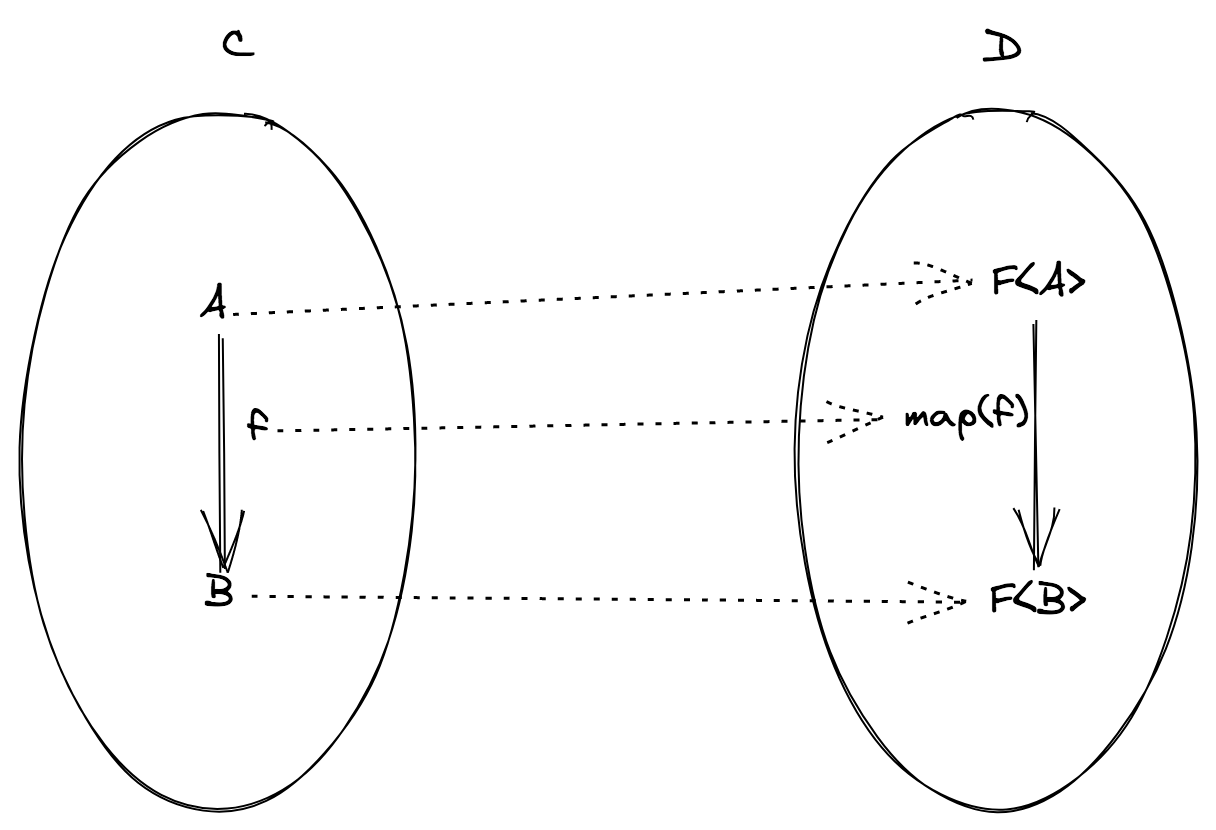
서로 다른 두 프로그래밍 언어의 매핑은 굉장한 아이디어지만, 우리는 C 와 D 가 동일한 상황(TS category) 에서의 매핑에 더 관심이 있습니다. 이 경우에는 endofunctors 라고 부릅니다 (그리스어 "endo" 는 "내부" 를 뜻합니다)
앞으로 따로 설명하지 않는한 "functor" 는 TS category 에서의 endofunctor 를 의미합니다.
이제 functor 의 실용적인 면을 알게 되었으니, 공식 정의를 살펴봅시다.
정의
functor 는 다음을 만족하는 쌍 (F, map) 입니다:
F는 한 개 이상의 파라미터를 가지는 type constructor 로 모든 타입X를F<X>로 매핑합니다 (object 간의 매핑)map은 다음 시그니쳐를 가진 함수입니다:
map: <A, B>(f: (a: A) => B) => ((fa: F<A>) => F<B>)
이 함수는 모든 함수 f: (a: A) => B 를 map(f): (fa: F<A>) => F<B> 로 매핑합니다 (morphism 간의 매핑)
다음 두 성질을 만족해야 합니다:
map(1X)=1F(X) (항등원은 항등원으로 매핑됩니다)map(g ∘ f) = map(g) ∘ map(f)(합성의 상(image)는 상들의 합성과 동일합니다)
두 번째 법칙은 다음과 같은 상황에서 계산을 최적화할 때 사용할 수 있습니다:
import { flow, increment, pipe } from 'fp-ts/function'
import { map } from 'fp-ts/ReadonlyArray'
const double = (n: number): number => n * 2
// 배열을 두 번 순회합니다
console.log(pipe([1, 2, 3], map(double), map(increment))) // => [ 3, 5, 7 ]
// 배열을 한 번 순회합니다
console.log(pipe([1, 2, 3], map(flow(double, increment)))) // => [ 3, 5, 7 ]
Functor 와 함수형 에러처리
Functor 는 함수형 에러처리에 긍적적인 효과를 발휘합니다: 다음 실용적인 예제를 살펴봅시다:
declare const doSomethingWithIndex: (index: number) => string
export const program = (ns: ReadonlyArray<number>): string => {
// -1 는 원하는 요소가 없다는 것을 의미합니다
const i = ns.findIndex((n) => n > 0)
if (i !== -1) {
return doSomethingWithIndex(i)
}
throw new Error('양수를 찾을 수 없습니다')
}
기본 findIndex API 를 사용하면 결과가 -1 이 아닌지 확인해야 하는 if 문을 무조건 사용해야합니다. 만약 깜박한 경우, doSomethingWithIndex 에 의도하지 않은 입력인 -1 을 전달할 수 있습니다.
Option 과 해당 functor 인스턴스를 사용해 동일한 결과를 얻는 것이 얼마나 쉬운지 살펴봅시다:
import { pipe } from 'fp-ts/function'
import { map, Option } from 'fp-ts/Option'
import { findIndex } from 'fp-ts/ReadonlyArray'
declare const doSomethingWithIndex: (index: number) => string
export const program = (ns: ReadonlyArray<number>): Option<string> =>
pipe(
ns,
findIndex((n) => n > 0),
map(doSomethingWithIndex)
)
Option 을 사용하면, 우리는 happy path 에 대해서만 생각할 수 있으며, 에러처리는 map 안에서 내부적으로 이뤄집니다.
데모 (optional)
문제. Task<A> 는 항상 성공하는 비동기 호출을 의미합니다. 그렇다면 실패할 수 있는 계산작업은 어떻게 모델링할까요?
Functor 합성
Functor 합성이란, 주어진 두 개의 functor F 와 G 를 합성한 F<G<A>> 를 말하며 이 또한 functor 입니다. 여기서 합성한 functor 의 map 함수는 각 functor 의 map 함수의 합성입니다.
예제 (F = Task, G = Option)
import { flow } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as T from 'fp-ts/Task'
type TaskOption<A> = T.Task<O.Option<A>>
export const map: <A, B>(
f: (a: A) => B
) => (fa: TaskOption<A>) => TaskOption<B> = flow(O.map, T.map)
// -------------------
// 사용 예제
// -------------------
interface User {
readonly id: number
readonly name: string
}
// 더미 원격 데이터베이스
const database: Record<number, User> = {
1: { id: 1, name: 'Ruth R. Gonzalez' },
2: { id: 2, name: 'Terry R. Emerson' },
3: { id: 3, name: 'Marsha J. Joslyn' }
}
const getUser = (id: number): TaskOption<User> => () =>
Promise.resolve(O.fromNullable(database[id]))
const getName = (user: User): string => user.name
// getUserName: number -> TaskOption<string>
const getUserName = flow(getUser, map(getName))
getUserName(1)().then(console.log) // => some('Ruth R. Gonzalez')
getUserName(4)().then(console.log) // => none
Contravariant Functors
사실 이전 장에서 우리는 정의를 완전히 철저히 따지지 않았습니다. 이전 장에서 "functor" 는 covariant (공변) functor 라고 부르는게 적절합니다.
이번 장에서 우리는 또 다른 functor 인 contravariant (반변) functor 를 살펴보려 합니다.
contravariant functor 의 정의는 기본 연산의 시그니쳐를 제외하면 covariant 와 거의 동일합니다. 해당 연산은 map 보다는 contramap 으로 불립니다.
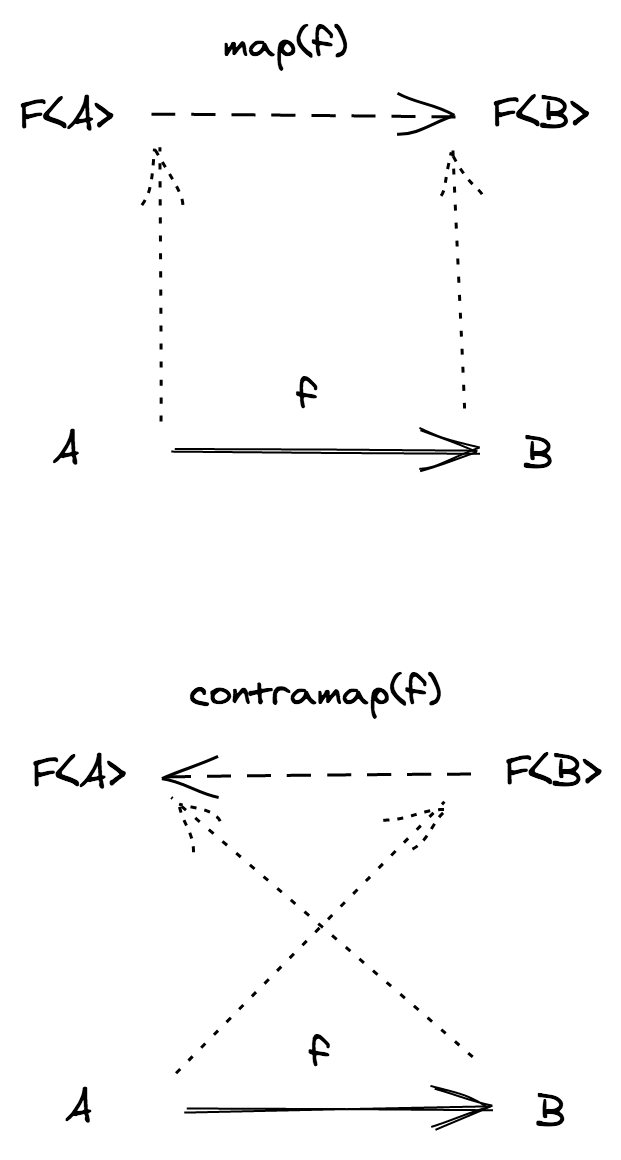
예제
import { map } from 'fp-ts/Option'
import { contramap } from 'fp-ts/Eq'
type User = {
readonly id: number
readonly name: string
}
const getId = (_: User): number => _.id
//`map` 이 동작하는 방식입니다
// const getIdOption: (fa: Option<User>) => Option<number>
const getIdOption = map(getId)
// `contramap` 이 동작하는 방식입니다
// const getIdEq: (fa: Eq<number>) => Eq<User>
const getIdEq = contramap(getId)
import * as N from 'fp-ts/number'
const EqID = getIdEq(N.Eq)
/*
이전 `Eq` 챕터에서 확인한 내용입니다:
const EqID: Eq<User> = pipe(
N.Eq,
contramap((_: User) => _.id)
)
*/
fp-ts 에서의 functor
fp-ts 에서는 어떻게 functor 를 정의할까요? 예제를 살펴봅시다.
다음 인터페이스는 어떤 HTTP API 의 결과를 표현한 것입니다:
interface Response<A> {
url: string
status: number
headers: Record<string, string>
body: A
}
boby 는 타입 파라미터를 받기 때문에 이는 Response 가 functor 인스턴스의 후보가 된다는 것을 확인해주세요. 즉 Response 는 n 개의 파라미터를 받는 type constructor 조건을 만족합니다. (필요조건)
Response 의 functor 인스턴스를 만들기 위해, fp-ts 가 요구하는 기술적인 상세 와 함께 map 함수를 정의해야 합니다.
// `Response.ts` module
import { pipe } from 'fp-ts/function'
import { Functor1 } from 'fp-ts/Functor'
declare module 'fp-ts/HKT' {
interface URItoKind<A> {
readonly Response: Response<A>
}
}
export interface Response<A> {
readonly url: string
readonly status: number
readonly headers: Record<string, string>
readonly body: A
}
export const map = <A, B>(f: (a: A) => B) => (
fa: Response<A>
): Response<B> => ({
...fa,
body: f(fa.body)
})
// `Response<A>` 의 functor 인스턴스
export const Functor: Functor1<'Response'> = {
URI: 'Response',
map: (fa, f) => pipe(fa, map(f))
}
이제 functor 로 일반적인 문제를 해결할 수 있나요?
아직 아닙니다. Functor 는 effectful 프로그램인 f 를 순수 함수인 g 를 합성할 수 있게 해줍니다. 하지만 g 는 오직 하나의 인자를 받은 unary 함수이어야 합니다. 만약 g 가 두 개 이상의 인자를 받는다면 어떻게 될까요?
| 프로그램 f | 프로그램 g | 합성 |
|---|---|---|
| pure | pure | g ∘ f |
| effectful | pure (unary) | map(g) ∘ f |
| effectful | pure (n-ary, n > 1) | ? |
이 상황을 해결하려면 무언가 더 필요합니다. 다음 장에서 함수형 프로그래밍에서 또 다른 중요한 추상화인 applicative functor 를 살펴볼 예정입니다.
Applicative functors
Functor 섹션에서 effectful 프로그램 인 f: (a: A) => F<B> 와 순수함수 g: (b: B) => C 를 합성하기 위해 g 를 map(g): (fb: F<B>) => F<C> 처럼 변형시킨 과정을 살펴보았습니다. (F 는 functor 인스턴스)
| 프로그램 f | 프로그램 g | 합성 |
|---|---|---|
| pure | pure | g ∘ f |
| effectful | pure (unary) | map(g) ∘ f |
하지만 g 는 한 개의 파라미터를 받는 unary 함수이어야 합니다. 만약 g 가 두 개를 받는다면 어떻게 될까요? 여전히 functor 인스턴스만 가지고 g 를 변형할 수 있을까요?
Currying
우선 타입 B 와 C (tuple 로 표현할 수 있습니다) 두 개의 인자를 받고 타입 D 를 반환하는 함수 모델링이 필요합니다.
g: (b: B, c: C) => D
currying 으로 불리는 기법을 사용해 g 를 다시 작성할 수 있습니다.
Currying 은 여러 개의 인자를 받는 함수의 평가를 각각 하나의 인자를 가진 일련의 함수들의 평가하는 것으로 변환하는 기술입니다. 예를 들어, 두 개의 인자
B와C를 받아D를 반환하는 함수를 currying 하면B하나를 받는 함수로 변환되며 해당 함수는C를 받아D를 반환하는 함수를 반환합니다.
(출처: wikipedia.org)
따라서, currying 을 통해 g 를 다음과 같이 작성할 수 있습니다:
g: (b: B) => (c: C) => D
예제
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const addFollower = (follower: User, user: User): User => ({
...user,
followers: [...user.followers, follower]
})
Currying 을 통해 addFollower 를 개선해봅시다
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const addFollower = (follower: User) => (user: User): User => ({
...user,
followers: [...user.followers, follower]
})
// -------------------
// 사용 예제
// -------------------
const user: User = { id: 1, name: 'Ruth R. Gonzalez', followers: [] }
const follower: User = { id: 3, name: 'Marsha J. Joslyn', followers: [] }
console.log(addFollower(follower)(user))
/*
{
id: 1,
name: 'Ruth R. Gonzalez',
followers: [ { id: 3, name: 'Marsha J. Joslyn', followers: [] } ]
}
*/
ap 연산
다음과 같은 상황을 가정합시다:
follower는 없지만 그의id를 가지고 있습니다user는 없지만 그의id를 가지고 있습니다- 주어진
id에 대한User를 가져오는fetchUserAPI 가 있습니다
import * as T from 'fp-ts/Task'
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const addFollower = (follower: User) => (user: User): User => ({
...user,
followers: [...user.followers, follower]
})
declare const fetchUser: (id: number) => T.Task<User>
const userId = 1
const followerId = 3
const result = addFollower(fetchUser(followerId))(fetchUser(userId)) // 컴파일 되지 않습니다
더이상 addFollower 를 사용할 수 없습니다! 어떻게 해야할까요?
다음 시그니쳐를 가진 함수만 있으면 가능할거 같습니다:
declare const addFollowerAsync: (
follower: T.Task<User>
) => (user: T.Task<User>) => T.Task<User>
그러면 다음과 같이 진행할 수 있습니다:
import * as T from 'fp-ts/Task'
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
declare const fetchUser: (id: number) => T.Task<User>
declare const addFollowerAsync: (
follower: T.Task<User>
) => (user: T.Task<User>) => T.Task<User>
const userId = 1
const followerId = 3
// const result: T.Task<User>
const result = addFollowerAsync(fetchUser(followerId))(fetchUser(userId)) // 컴파일 됩니다
물론 직접 addFollowerAsyn 를 구현할 수 있습니다만, 함수 addFollower: (follower: User) => (user: User): User 에서 시작해 함수 addFollowerAsync: (follower: Task<User>) => (user: Task<User>) => Task<User> 로 만드는 변환을 찾는게 가능할까요?
더 일반적으로, 우리가 원하는 것은 liftA2 라고 불리는 변환이며, 함수 g: (b: B) => (c: C) => D 에서 다음과 같은 시그니쳐를 가진 함수를 반환합니다:
liftA2(g): (fb: F<B>) => (fc: F<C>) => F<D>
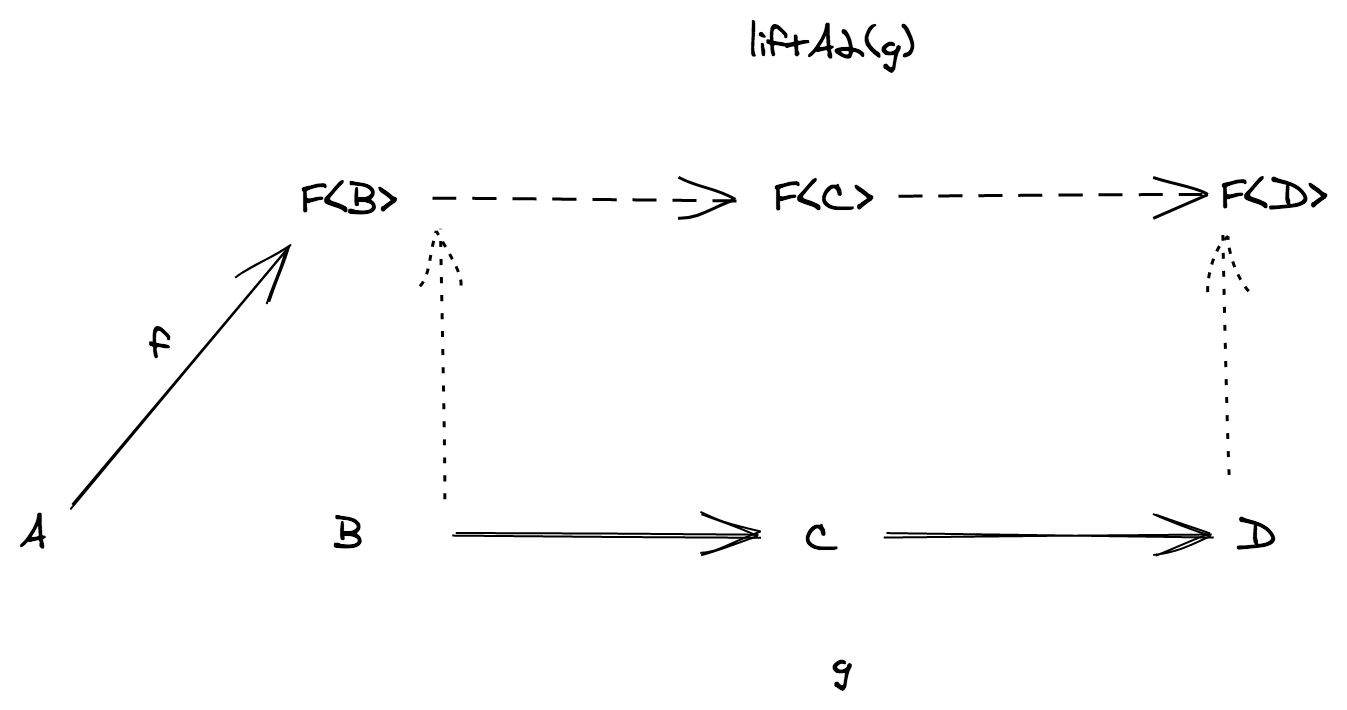
어떻게 구할 수 있을까요? 주어진 g 는 unary 함수이므로, functor 인스턴스와 map 을 활용할 수 있습니다:
map(g): (fb: F<B>) => F<(c: C) => D>
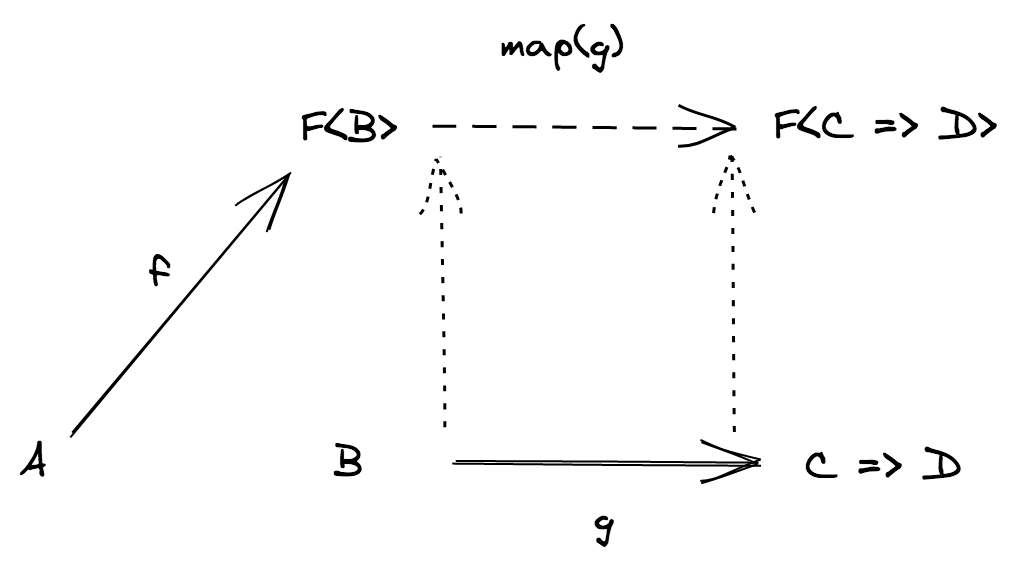
이제 문제가 발생합니다: functor 인스턴스는 타입 F<(c: C) => D> 에서 (fc: F<C>) => F<D> 로 만드는 연산을 지원하지 않습니다.
이제 이 기능을 위한 새로운 연산인 ap 를 도입할 필요가 있습니다:
declare const ap: <A>(fa: Task<A>) => <B>(fab: Task<(a: A) => B>) => Task<B>
참고. 왜 이름이 "ap" 일까요? 왜냐하면 마치 함수 적용과 같은 형태를 보이기 때문입니다.
// `apply` 는 값을 함수에 적용합니다
declare const apply: <A>(a: A) => <B>(f: (a: A) => B) => B
declare const ap: <A>(a: Task<A>) => <B>(f: Task<(a: A) => B>) => Task<B>
// `ap` 는 effect 에 감싸진 값을 effect 에 감싸진 함수에 적용합니다
이제 ap 가 있으니 liftA2 를 정의할 수 있습니다:
import { pipe } from 'fp-ts/function'
import * as T from 'fp-ts/Task'
const liftA2 = <B, C, D>(g: (b: B) => (c: C) => D) => (fb: T.Task<B>) => (
fc: T.Task<C>
): T.Task<D> => pipe(fb, T.map(g), T.ap(fc))
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const addFollower = (follower: User) => (user: User): User => ({
...user,
followers: [...user.followers, follower]
})
// const addFollowerAsync: (fb: T.Task<User>) => (fc: T.Task<User>) => T.Task<User>
const addFollowerAsync = liftA2(addFollower)
마침내, 우리는 이전 결과에서 fetchUser 를 합성할 수 있습니다:
import { flow, pipe } from 'fp-ts/function'
import * as T from 'fp-ts/Task'
const liftA2 = <B, C, D>(g: (b: B) => (c: C) => D) => (fb: T.Task<B>) => (
fc: T.Task<C>
): T.Task<D> => pipe(fb, T.map(g), T.ap(fc))
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const addFollower = (follower: User) => (user: User): User => ({
...user,
followers: [...user.followers, follower]
})
declare const fetchUser: (id: number) => T.Task<User>
// const program: (id: number) => (fc: T.Task<User>) => T.Task<User>
const program = flow(fetchUser, liftA2(addFollower))
const userId = 1
const followerId = 3
// const result: T.Task<User>
const result = program(followerId)(fetchUser(userId))
이제 두 함수 f: (a: A) => F<B> 와 g: (b: B, c: C) => D 를 합성하는 표준적 절차를 얻었습니다:
We have found a standard procedure to compose two functions f: (a: A) => F<B>, g: (b: B, c: C) => D:
g를 currying 을 통해 함수g: (b: B) => (c: C) => D로 변환합니다- Effect
F를 위한ap함수를 정의합니다 (라이브러리 함수) - Effect
F를 위한liftA2함수를 정의합니다 (라이브러리 함수) - 다음 합성을 수행합니다
flow(f, liftA2(g))
이전에 본 type constructor 일부에 대한 ap 연산의 구현을 살펴봅시다:
예제 (F = ReadonlyArray)
import { increment, pipe } from 'fp-ts/function'
const ap = <A>(fa: ReadonlyArray<A>) => <B>(
fab: ReadonlyArray<(a: A) => B>
): ReadonlyArray<B> => {
const out: Array<B> = []
for (const f of fab) {
for (const a of fa) {
out.push(f(a))
}
}
return out
}
const double = (n: number): number => n * 2
pipe([double, increment], ap([1, 2, 3]), console.log) // => [ 2, 4, 6, 2, 3, 4 ]
예제 (F = Option)
import { pipe } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
const ap = <A>(fa: O.Option<A>) => <B>(
fab: O.Option<(a: A) => B>
): O.Option<B> =>
pipe(
fab,
O.match(
() => O.none,
(f) =>
pipe(
fa,
O.match(
() => O.none,
(a) => O.some(f(a))
)
)
)
)
const double = (n: number): number => n * 2
pipe(O.some(double), ap(O.some(1)), console.log) // => some(2)
pipe(O.some(double), ap(O.none), console.log) // => none
pipe(O.none, ap(O.some(1)), console.log) // => none
pipe(O.none, ap(O.none), console.log) // => none
예제 (F = IO)
import { IO } from 'fp-ts/IO'
const ap = <A>(fa: IO<A>) => <B>(fab: IO<(a: A) => B>): IO<B> => () => {
const f = fab()
const a = fa()
return f(a)
}
예제 (F = Task)
import { Task } from 'fp-ts/Task'
const ap = <A>(fa: Task<A>) => <B>(fab: Task<(a: A) => B>): Task<B> => () =>
Promise.all([fab(), fa()]).then(([f, a]) => f(a))
예제 (F = Reader)
import { Reader } from 'fp-ts/Reader'
const ap = <R, A>(fa: Reader<R, A>) => <B>(
fab: Reader<R, (a: A) => B>
): Reader<R, B> => (r) => {
const f = fab(r)
const a = fa(r)
return f(a)
}
지금까지 ap 가 두 개의 파라미터를 받는 함수를 다루는 것을 보았습니다. 하지만 함수가 세 개의 파라미터를 받는다면 어떡할까요? 또 다른 추상화 가 필요할까요?
다행이도 필요하지 않습니다. map 과 ap 만으로 충분합니다:
import { pipe } from 'fp-ts/function'
import * as T from 'fp-ts/Task'
const liftA3 = <B, C, D, E>(f: (b: B) => (c: C) => (d: D) => E) => (
fb: T.Task<B>
) => (fc: T.Task<C>) => (fd: T.Task<D>): T.Task<E> =>
pipe(fb, T.map(f), T.ap(fc), T.ap(fd))
const liftA4 = <B, C, D, E, F>(
f: (b: B) => (c: C) => (d: D) => (e: E) => F
) => (fb: T.Task<B>) => (fc: T.Task<C>) => (fd: T.Task<D>) => (
fe: T.Task<E>
): T.Task<F> => pipe(fb, T.map(f), T.ap(fc), T.ap(fd), T.ap(fe))
// etc...
이제 "합성 테이블" 을 수정할 수 있습니다:
| 프로그램 f | 프로그램 g | 합성 |
|---|---|---|
| pure | pure | g ∘ f |
| effectful | pure (unary) | map(g) ∘ f |
| effectful | pure, n-ary | liftAn(g) ∘ f |
of 연산
이제 다음 두 함수 f: (a: A) => F<B>, g: (b: B, c: C) => D 에서 다음 합성 h 을 얻을 수 있음을 보았습니다:
h: (a: A) => (fb: F<B>) => F<D>
h 를 실행하기 위해 타입 A 의 값과 타입 F<B> 의 값이 필요합니다.
하지만 만약, 두 번째 파라미터 fb 를 위한 타입 F<B> 의 값 대신 B 만 가지고 있다면 어떡할까요?
B 를 F<B> 로 바꿔주는 연산이 있다면 유용할 것입니다.
이제 그러한 역할을 하는 of 로 불리는 연산을 소개합니다 (동의어: pure, return):
declare const of: <B>(b: B) => F<B>
보통 ap 와 of 연산을 가지는 type constructor 에 대해서만 applicative functors 라는 용어를 사용합니다.
지금까지 살펴본 type constructor 에 대한 of 의 정의를 살펴봅시다:
예제 (F = ReadonlyArray)
const of = <A>(a: A): ReadonlyArray<A> => [a]
예제 (F = Option)
import * as O from 'fp-ts/Option'
const of = <A>(a: A): O.Option<A> => O.some(a)
예제 (F = IO)
import { IO } from 'fp-ts/IO'
const of = <A>(a: A): IO<A> => () => a
예제 (F = Task)
import { Task } from 'fp-ts/Task'
const of = <A>(a: A): Task<A> => () => Promise.resolve(a)
예제 (F = Reader)
import { Reader } from 'fp-ts/Reader'
const of = <R, A>(a: A): Reader<R, A> => () => a
데모
Applicative functors 합성
Applicative functors 합성이란, 두 applicative functor F 와 G 에 대해 F<G<A>> 또한 applicative functor 라는 것을 말합니다.
예제 (F = Task, G = Option)
합성의 of 는 각 of 의 합성과 같습니다:
import { flow } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as T from 'fp-ts/Task'
type TaskOption<A> = T.Task<O.Option<A>>
const of: <A>(a: A) => TaskOption<A> = flow(O.of, T.of)
합성의 ap 는 다음 패턴을 활용해 얻을 수 있습니다:
const ap = <A>(
fa: TaskOption<A>
): (<B>(fab: TaskOption<(a: A) => B>) => TaskOption<B>) =>
flow(
T.map((gab) => (ga: O.Option<A>) => O.ap(ga)(gab)),
T.ap(fa)
)
이제 applicative functors 로 일반적인 문제를 해결할 수 있나요?
아직 아닙니다. 이제 마지막으로 가장 중요한 경우를 고려해야합니다. 두 프로그램 모두 effectful 할 때 입니다.
아직 무언가 더 필요합니다. 다음 장에서 함수형 프로그래밍에서 가장 중요한 추상화 중 하나인 monad 를 살펴볼 예정입니다.
Monads

(Eugenio Moggi 는 이탈리아 Genoa 대학교의 컴퓨터 공학 교수입니다. 그는 먼저 프로그램을 만들기 위한 monad 의 일반적인 사용법을 발견했습니다)

(Philip Lee Wadler 는 프로그래밍 언어 디자인과 타입 이론에 기여한 것으로 알려진 미국의 컴퓨터 과학자입니다)
이전 장에서 type constructor F 가 applicative functor 인스턴스를 가지는 경우에만 1 개 이상의 파라미터를 가지는 순수 프로그램 g 와 effectful 프로그램 f: (a: A) => F<B> 를 합성할 수 있음을 살펴보았습니다:
| 프로그램 f | 프로그램 g | 합성 |
|---|---|---|
| pure | pure | g ∘ f |
| effectful | pure (unary) | map(g) ∘ f |
| effectful | pure, n-ary | liftAn(g) ∘ f |
하지만 꽤 자주 발생하는 다음 상황에 대한 문제를 해결해야합니다. 두 프로그램 모두 effectful 인 경우입니다:
f: (a: A) => F<B>
g: (b: B) => F<C>
f 와 g 의 합성이란 무엇일까요?
중첩된 context 문제
일반적인 문제를 풀기 위해 무언가 더 필요한 이유를 보여주는 몇가지 예제를 살펴봅시다.
예제 (F = Array)
Follower 들의 follower 가 필요한 상황이라 가정합시다.
import { pipe } from 'fp-ts/function'
import * as A from 'fp-ts/ReadonlyArray'
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const getFollowers = (user: User): ReadonlyArray<User> => user.followers
declare const user: User
// followersOfFollowers: ReadonlyArray<ReadonlyArray<User>>
const followersOfFollowers = pipe(user, getFollowers, A.map(getFollowers))
여기서 문제가 발생합니다, followersOfFollowers 의 타입은 ReadonlyArray<ReadonlyArray<User>> 이지만 우리가 원하는 것은 ReadonlyArray<User> 입니다.
중첩된 배열의 평탄화(flatten) 가 필요합니다.
fp-ts/ReadonlyArray 모듈에 있는 함수 flatten: <A>(mma: ReadonlyArray<ReadonlyArray<A>>) => ReadonlyArray<A> 가 바로 우리가 원하는 것입니다:
// followersOfFollowers: ReadonlyArray<User>
const followersOfFollowers = pipe(
user,
getFollowers,
A.map(getFollowers),
A.flatten
)
좋습니다! 다른 자료형도 살펴봅시다.
예제 (F = Option)
숫자 배열의 첫 번째 요소의 역수를 계산한다고 가정합시다:
import { pipe } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as A from 'fp-ts/ReadonlyArray'
const inverse = (n: number): O.Option<number> =>
n === 0 ? O.none : O.some(1 / n)
// inverseHead: O.Option<O.Option<number>>
const inverseHead = pipe([1, 2, 3], A.head, O.map(inverse))
이런, 같은 현상이 발생합니다, inverseHead 의 타입은 Option<Option<number>> 이지만 우리가 원하는 것은 Option<number> 입니다.
이번에도 중첩된 Option 를 평평하게 만들어야 합니다.
fp-ts/Option 모듈에 있는 함수 flatten: <A>(mma: Option<Option<A>>) => Option<A> 가 우리가 원하는 것입니다:
// inverseHead: O.Option<number>
const inverseHead = pipe([1, 2, 3], A.head, O.map(inverse), O.flatten)
모든 곳에 flatten 함수가 있는데... 이것은 우연은 아닙니다. 다음과 같은 함수형 패턴이 존재합니다:
두 type constructor ReadonlyArray 와 Option (그 외 여러) 은 monad 인스턴스 를 가지고 있습니다.
flatten은 monad 의 가장 특별한 연산입니다
참고. flatten 의 자주 사용되는 동의어로 join 이 있습니다.
그럼 monad 란 무엇일까요?
보통 다음과 같이 표현합니다...
Monad 정의
정의. Monad 는 다음 세 가지 항목으로 정의합니다:
(1) Functor 인스턴스를 만족하는 type constructor M
(2) 다음 시그니처를 가진 (pure 나 return 으로도 불리는) 함수 of:
of: <A>(a: A) => M<A>
(3) 다음 시그니처를 가진 (flatMap 이나 bind 로도 불리는) 함수 chain:
chain: <A, B>(f: (a: A) => M<B>) => (ma: M<A>) => M<B>
of 와 chain 함수는 아래 세 가지 법칙을 만족해야 합니다:
chain(of) ∘ f = f(좌동등성)chain(f) ∘ of = f(우동등성)chain(h) ∘ (chain(g) ∘ f) = chain((chain(h) ∘ g)) ∘ f(결합법칙)
여기서 f, g, h 는 모두 effectful 함수이며 ∘ 는 보통의 함수 합성을 말합니다.
처음 이 정의를 보았을 때 많은 의문이 생겼습니다:
of와chain연산이란 무엇인가? 왜 그러한 시그니처를 가지고 있는가?- 왜 "pure" 나 "flatMap" 와 같은 동의어를 가지고 있는가?
- 왜 그러한 법칙을 만족해야 하는가? 그것은 무엇을 의미하는가?
flatten이 monad 에서 그렇게 중요하다면, 왜 정의에는 보이지 않는걸까?
이번 장에서 위 의문들을 모두 해소할 것입니다.
핵심 문제로 돌아가봅시다: 두 effectful 함수 f 와 g 의 합성이란 무엇일까요?
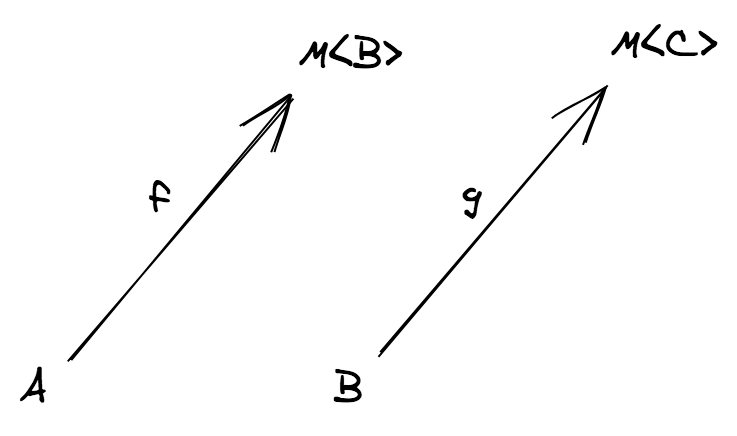
참고. Effectful 함수는 Kleisli arrow 라고도 불립니다.
당분간은 그러한 합성의 타입 조차 알지 못합니다.
하지만 우리는 이미 합성에 대해 구체적으로 이야기하는 추상적인 개념들을 살펴보았습니다. 우리가 category 에 대해 말했던 것을 기억하나요?
category 는 합성의 본질이라 할 수 있습니다.
우리는 당면한 문제를 category 문제로 바꿀 수 있습니다: Kleisli arrows 의 합성을 모델링하는 category 를 찾을 수 있을까요?
Kleisli category

Kleisli arrow 로만 이루어진 (Kleisli category 로 불리는) category K 를 만들어봅시다:
- object 는 TS category 에서의 object 와 동일합니다, 즉 모든 TypeScript 타입입니다.
- morphism 은 다음 방식으로 만듭니다: TS 에서의 모든 Kleisli arrow
f: A ⟼ M<B>는 K 에서f': A ⟼ B로 매핑됩니다.
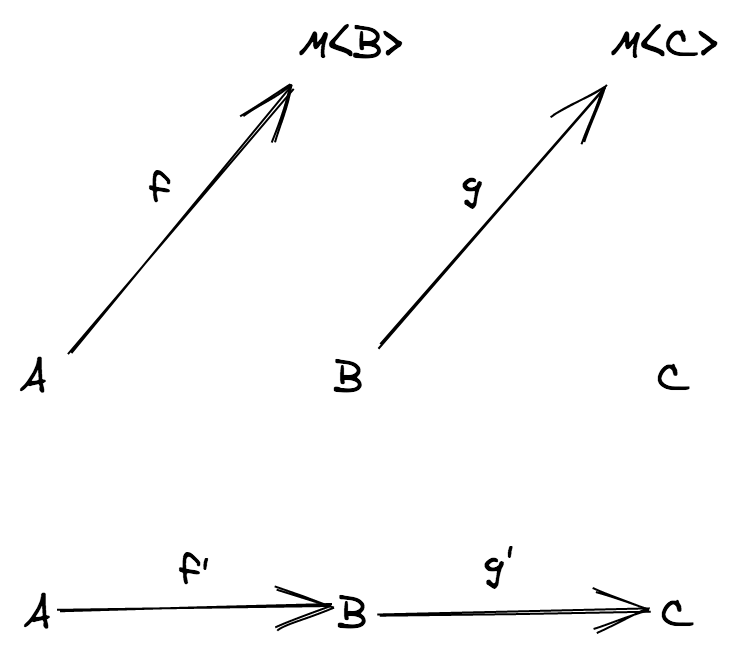
그렇다면 K 에서 f 와 g 의 합성은 무엇일까요? 아래 아미지에서 h' 로 표시된 붉은 화살표입니다:
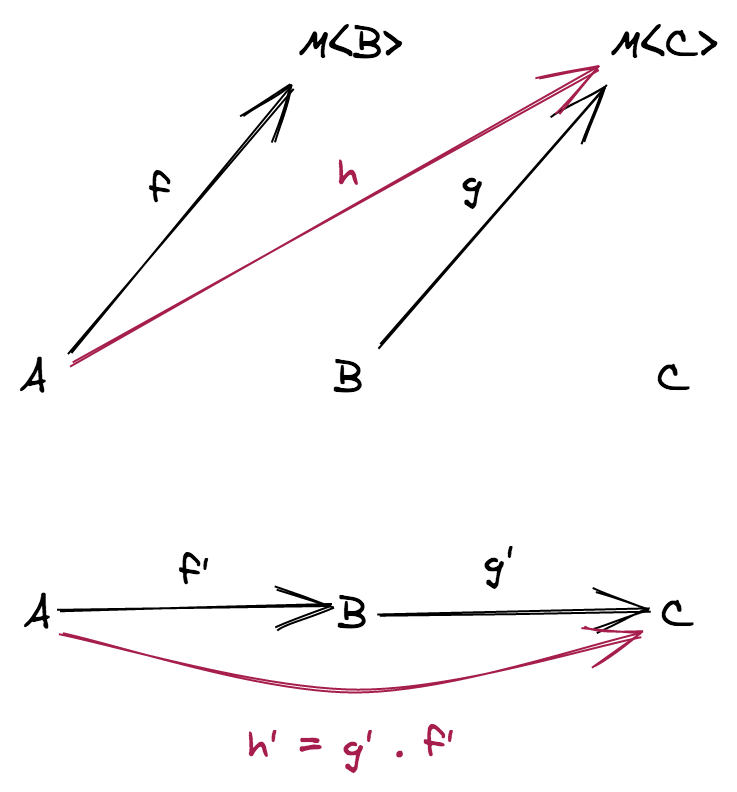
K 에 속하는 A 에서 C 로 향하는 화살표 h' 가 주어지면, 그에 해당하는 TS 에 속하는 A 에서 M<C> 로 향하는 함수 h 를 찾을 수 있습니다.
따라서 TS 에서 f 와 g 의 합성을 위한 좋은 후보는 다음 시그니처를 가진 Kleisli arrow 입니다: (a: A) => M<C>
이제 이러한 함수를 구현해봅시다.
단계별 chain 정의하기
Monad 의 첫 번째 정의는 M 은 functor 인스턴스를 만족해야 함을 의미하며 g: (b: B) => M<C> 함수를 map(g): (mb: M<B>) => M<M<C>> 로 변경할 수 있다는 사실을 알 수 있습니다.
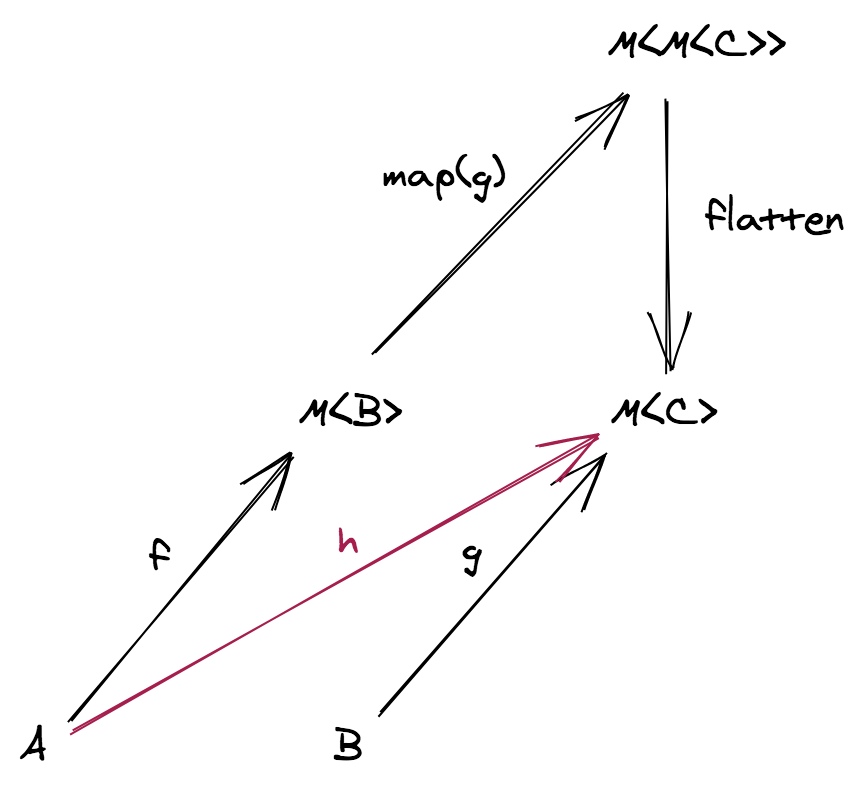
이제 문제가 발생합니다: functor 인스턴스를 위한 M<M<C>> 타입을 M<C> 로 만들어주는 연산이 필요한 상황이며 그러한 연산자를 flatten 이라 부르도록 합시다.
만약 이 연산자를 정의할 수 있다면 우리가 원하는 합성 방법을 찾을 수 있습니다:
h = flatten ∘ map(g) ∘ f
flatten ∘ map(g) 이름을 합쳐서 "flatMap" 이라는 이름을 얻을 수 있습니다!
chain 도 이 방식으로 얻을 수 있습니다
chain = flatten ∘ map(g)
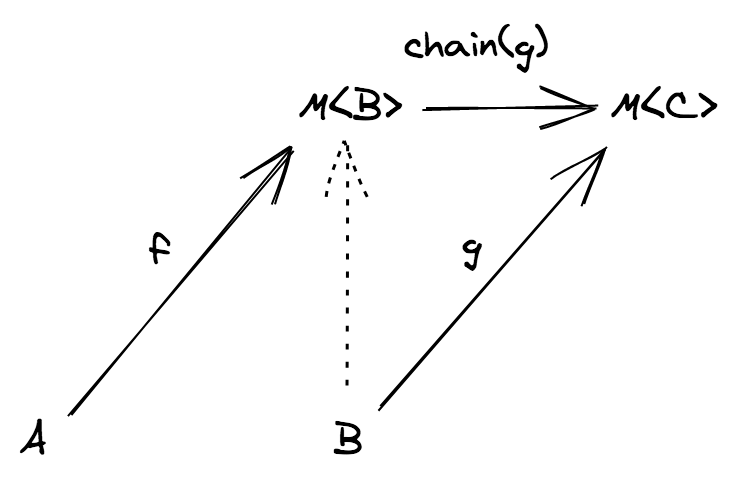
이제 합성 테이블을 갱신할 수 있습니다
| 프로그램 f | 프로그램 g | 합성 |
|---|---|---|
| pure | pure | g ∘ f |
| effectful | pure (unary) | map(g) ∘ f |
| effectful | pure, n-ary | liftAn(g) ∘ f |
| effectful | effectful | chain(g) ∘ f |
of 는 경우는 어떤가요? 사실 of 는 K 의 identity morphism 에서 왔습니다. K 의 임의의 identity morphism 인 1A 에 대해 A 에서 M<A> 로 매칭되는 함수가 존재합니다 (즉 of: <A>(a: A) => M<A>).
(원문) What about
of? Well,ofcomes from the identity morphisms in K: for every identity morphism 1A in K there has to be a corresponding function fromAtoM<A>(that is,of: <A>(a: A) => M<A>).
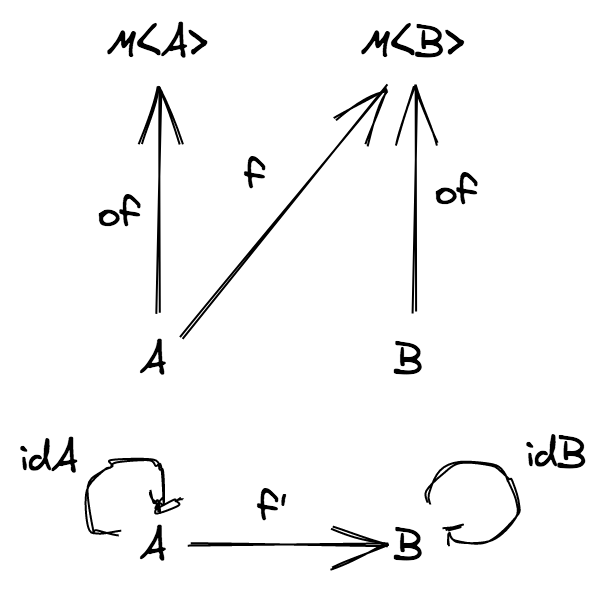
of 가 chain 에 대한 중립 원소라는 사실은 다음과 같은 종류의 흐름 제어를 가능하게 합니다:
pipe(
mb,
M.chain((b) => (predicate(b) ? M.of(b) : g(b)))
)
여기서 predicate: (b: B) => boolean, mb: M<B> 이며 g: (b: B) => M<B>.
마지막 질문: Monad 법칙은 어디에서 온걸까요? 법칙은 단순히 K 에서의 범주형 법칙이 TS 로 변환된 것입니다:
| Law | K | TS |
|---|---|---|
| 좌동등성 | 1B ∘ f' = f' | chain(of) ∘ f = f |
| 우동등성 | f' ∘ 1A = f' | chain(f) ∘ of = f |
| 결합법칙 | h' ∘ (g' ∘ f') = (h' ∘ g') ∘ f' | chain(h) ∘ (chain(g) ∘ f) = chain((chain(h) ∘ g)) ∘ f |
이제 이전에 본 중첩된 context 문제를 chain 을 통해 해결할 수 있습니다:
import { pipe } from 'fp-ts/function'
import * as O from 'fp-ts/Option'
import * as A from 'fp-ts/ReadonlyArray'
interface User {
readonly id: number
readonly name: string
readonly followers: ReadonlyArray<User>
}
const getFollowers = (user: User): ReadonlyArray<User> => user.followers
declare const user: User
const followersOfFollowers: ReadonlyArray<User> = pipe(
user,
getFollowers,
A.chain(getFollowers)
)
const inverse = (n: number): O.Option<number> =>
n === 0 ? O.none : O.some(1 / n)
const inverseHead: O.Option<number> = pipe([1, 2, 3], A.head, O.chain(inverse))
지금까지 보았던 type constructor 에 대해 chain 함수를 어떻게 구현했는지 살펴봅시다:
예제 (F = ReadonlyArray)
// 함수 `B -> ReadonlyArray<C>` 를 함수 `ReadonlyArray<B> -> ReadonlyArray<C>` 로 변환합니다
const chain = <B, C>(g: (b: B) => ReadonlyArray<C>) => (
mb: ReadonlyArray<B>
): ReadonlyArray<C> => {
const out: Array<C> = []
for (const b of mb) {
out.push(...g(b))
}
return out
}
예제 (F = Option)
import { match, none, Option } from 'fp-ts/Option'
// 함수 `B -> Option<C>` 를 함수 `Option<B> -> Option<C>` 로 변환합니다
const chain = <B, C>(g: (b: B) => Option<C>): ((mb: Option<B>) => Option<C>) =>
match(() => none, g)
에제 (F = IO)
import { IO } from 'fp-ts/IO'
// 함수 `B -> IO<C>` 를 함수 `IO<B> -> IO<C>` 로 변환합니다
const chain = <B, C>(g: (b: B) => IO<C>) => (mb: IO<B>): IO<C> => () =>
g(mb())()
예제 (F = Task)
import { Task } from 'fp-ts/Task'
// 함수 `B -> Task<C>` 를 함수 `Task<B> -> Task<C>` 로 변환합니다
const chain = <B, C>(g: (b: B) => Task<C>) => (mb: Task<B>): Task<C> => () =>
mb().then((b) => g(b)())
예제 (F = Reader)
import { Reader } from 'fp-ts/Reader'
// 함수 `B -> Reader<R, C>` 를 함수 `Reader<R, B> -> Reader<R, C>` 로 변환합니다
const chain = <B, R, C>(g: (b: B) => Reader<R, C>) => (
mb: Reader<R, B>
): Reader<R, C> => (r) => g(mb(r))(r)
프로그램 다루기
이제 참조 투명성과 monad 개념을 통해 프로그램을 어떻게 다루는지 살펴봅시다.
여기 파일을 읽고 쓰는 작은 프로그램이 있습니다:
import { log } from 'fp-ts/Console'
import { IO, chain } from 'fp-ts/IO'
import { pipe } from 'fp-ts/function'
import * as fs from 'fs'
// -----------------------------------------
// 라이브러리 함수
// -----------------------------------------
const readFile = (filename: string): IO<string> => () =>
fs.readFileSync(filename, 'utf-8')
const writeFile = (filename: string, data: string): IO<void> => () =>
fs.writeFileSync(filename, data, { encoding: 'utf-8' })
// 지금까지 살펴본 함수들을 통해 만든 API
const modifyFile = (filename: string, f: (s: string) => string): IO<void> =>
pipe(
readFile(filename),
chain((s) => writeFile(filename, f(s)))
)
// -----------------------------------------
// 프로그램
// -----------------------------------------
const program1 = pipe(
readFile('file.txt'),
chain(log),
chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
chain(() => readFile('file.txt')),
chain(log)
)
pipe(readFile('file.txt'), chain(log))
위 로직은 프로그램에서 여러번 반복됩니다, 하지만 참조 투명성은 해당 식을 상수로 만들 수 있음을 보장해줍니다:
const read = pipe(readFile('file.txt'), chain(log))
const modify = modifyFile('file.txt', (s) => s + '\n// eof')
const program2 = pipe(
read,
chain(() => modify),
chain(() => read)
)
또한 combinator 를 정의해 활용하면 코드를 더 간결하게 만들 수 있습니다.
const interleave = <A, B>(action: IO<A>, middle: IO<B>): IO<A> =>
pipe(
action,
chain(() => middle),
chain(() => action)
)
const program3 = interleave(read, modify)
또 다른 예제: IO 를 위한 Unix 의 time 명령어와 유사한 함수를 구현하기.
import * as IO from 'fp-ts/IO'
import { now } from 'fp-ts/Date'
import { log } from 'fp-ts/Console'
import { pipe } from 'fp-ts/function'
// 계산 시간을 밀리세컨드 단위로 로그를 남깁니다
export const time = <A>(ma: IO.IO<A>): IO.IO<A> =>
pipe(
now,
IO.chain((startMillis) =>
pipe(
ma,
IO.chain((a) =>
pipe(
now,
IO.chain((endMillis) =>
pipe(
log(`Elapsed: ${endMillis - startMillis}`),
IO.map(() => a)
)
)
)
)
)
)
)
여담. 보시다시피, chain 을 사용하면서 scope 를 유지하는 경우 장황한 코드가 만들어집니다.
monadic 스타일을 기본적으로 지원하는 언어에서는 이러한 상황을 쉽게 해결해주는 "do notation" 이라는 이름으로 통하는 문법을 제공합니다.
Haskell 을 예로들면
now :: IO Int
now = undefined -- Haskell 에서의 `undefined` 는 TypeScript 와 동일한 의미를 가집니다
log :: String -> IO ()
log = undefined
time :: IO a -> IO a
time ma = do
startMillis <- now
a <- ma
endMillis <- now
log ("Elapsed:" ++ show (endMillis - startMillis))
return a
TypeScript 에서는 이러한 문법을 지원하지 않지만, 비슷한 역할을 하는 로직을 구현할 수 있습니다:
import { log } from 'fp-ts/Console'
import { now } from 'fp-ts/Date'
import { pipe } from 'fp-ts/function'
import * as IO from 'fp-ts/IO'
// 계산 시간을 밀리세컨드 단위로 로그를 남깁니다
export const time = <A>(ma: IO.IO<A>): IO.IO<A> =>
pipe(
IO.Do,
IO.bind('startMillis', () => now),
IO.bind('a', () => ma),
IO.bind('endMillis', () => now),
IO.chainFirst(({ endMillis, startMillis }) =>
log(`Elapsed: ${endMillis - startMillis}`)
),
IO.map(({ a }) => a)
)
time combinator 를 활용한 예제를 살펴봅시다:
import { randomInt } from 'fp-ts/Random'
import { Monoid, concatAll } from 'fp-ts/Monoid'
import { replicate } from 'fp-ts/ReadonlyArray'
const fib = (n: number): number => (n <= 1 ? 1 : fib(n - 1) + fib(n - 2))
// 30 과 35 사이의 임의의 숫자를 인자로 `fib` 함수를 호출합니다
// 또한 입력과 출력을 로그에 남깁니다
const randomFib: IO.IO<void> = pipe(
randomInt(30, 35),
IO.chain((n) => log([n, fib(n)]))
)
// `IO<void>` 용 monoid 인스턴스
const MonoidIO: Monoid<IO.IO<void>> = {
concat: (first, second) => () => {
first()
second()
},
empty: IO.of(undefined)
}
// `mv` 연산을 `n` 번 수행합니다
const replicateIO = (n: number, mv: IO.IO<void>): IO.IO<void> =>
concatAll(MonoidIO)(replicate(n, mv))
// -------------------
// 사용 예제
// -------------------
time(replicateIO(3, randomFib))()
/*
[ 31, 2178309 ]
[ 33, 5702887 ]
[ 30, 1346269 ]
Elapsed: 89
*/
중간 로그를 남길수도 있습니다:
time(replicateIO(3, time(randomFib)))()
/*
[ 33, 5702887 ]
Elapsed: 54
[ 30, 1346269 ]
Elapsed: 13
[ 32, 3524578 ]
Elapsed: 39
Elapsed: 106
*/
Monadic 인터페이스 (map, of, chain) 의 활용에서 가장 흥미로운 측면은 프로그램이 필요한 의존성을 여러 계산을 연결하는 방식 과 함께 주입할 수 있다는 것입니다.
이를 확인하기 위해, 파일을 읽고 쓰는 프로그램을 개선해봅시다:
import { IO } from 'fp-ts/IO'
import { pipe } from 'fp-ts/function'
// -----------------------------------------
// 헥사고날 아키텍쳐에서 "port" 라고 부르는 Deps 인터페이스
// -----------------------------------------
interface Deps {
readonly readFile: (filename: string) => IO<string>
readonly writeFile: (filename: string, data: string) => IO<void>
readonly log: <A>(a: A) => IO<void>
readonly chain: <A, B>(f: (a: A) => IO<B>) => (ma: IO<A>) => IO<B>
}
// -----------------------------------------
// 프로그램
// -----------------------------------------
const program4 = (D: Deps) => {
const modifyFile = (filename: string, f: (s: string) => string) =>
pipe(
D.readFile(filename),
D.chain((s) => D.writeFile(filename, f(s)))
)
return pipe(
D.readFile('file.txt'),
D.chain(D.log),
D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
D.chain(() => D.readFile('file.txt')),
D.chain(D.log)
)
}
// -----------------------------------------
// 헥사고날 아키텍쳐에서 "adapter" 라 부르는 `Deps` 인스턴스
// -----------------------------------------
import * as fs from 'fs'
import { log } from 'fp-ts/Console'
import { chain } from 'fp-ts/IO'
const DepsSync: Deps = {
readFile: (filename) => () => fs.readFileSync(filename, 'utf-8'),
writeFile: (filename: string, data: string) => () =>
fs.writeFileSync(filename, data, { encoding: 'utf-8' }),
log,
chain
}
// 의존성 주입
program4(DepsSync)()
더 나아가, 우리는 프로그램이 실행하는 효과를 추상화할 수 있습니다. 바로 FileSystem 효과를 직접 정의하는 것입니다. (파일 시스템에 동작하는 읽기-쓰기를 의미하는 효과):
import { IO } from 'fp-ts/IO'
import { pipe } from 'fp-ts/function'
// -----------------------------------------
// 프로그램의 효과
// -----------------------------------------
interface FileSystem<A> extends IO<A> {}
// -----------------------------------------
// 의존성
// -----------------------------------------
interface Deps {
readonly readFile: (filename: string) => FileSystem<string>
readonly writeFile: (filename: string, data: string) => FileSystem<void>
readonly log: <A>(a: A) => FileSystem<void>
readonly chain: <A, B>(
f: (a: A) => FileSystem<B>
) => (ma: FileSystem<A>) => FileSystem<B>
}
// -----------------------------------------
// 프로그램
// -----------------------------------------
const program4 = (D: Deps) => {
const modifyFile = (filename: string, f: (s: string) => string) =>
pipe(
D.readFile(filename),
D.chain((s) => D.writeFile(filename, f(s)))
)
return pipe(
D.readFile('file.txt'),
D.chain(D.log),
D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
D.chain(() => D.readFile('file.txt')),
D.chain(D.log)
)
}
우리는 단순히 FileSystem 효과의 정의를 수정하기만 하면, 비동기적으로 실행하는 프로그램으로 변경할 수 있습니다.
// -----------------------------------------
// 프로그램의 효과
// -----------------------------------------
-interface FileSystem<A> extends IO<A> {}
+interface FileSystem<A> extends Task<A> {}
이제 남은 작업은 새로운 정의에 맞게 Deps 인스턴스를 수정하는 것입니다.
import { Task } from 'fp-ts/Task'
import { pipe } from 'fp-ts/function'
// -----------------------------------------
// 프로그램의 효과 (수정됨)
// -----------------------------------------
interface FileSystem<A> extends Task<A> {}
// -----------------------------------------
// 의존성 (수정 안됨)
// -----------------------------------------
interface Deps {
readonly readFile: (filename: string) => FileSystem<string>
readonly writeFile: (filename: string, data: string) => FileSystem<void>
readonly log: <A>(a: A) => FileSystem<void>
readonly chain: <A, B>(
f: (a: A) => FileSystem<B>
) => (ma: FileSystem<A>) => FileSystem<B>
}
// -----------------------------------------
// 프로그램 (수정 안됨)
// -----------------------------------------
const program5 = (D: Deps) => {
const modifyFile = (filename: string, f: (s: string) => string) =>
pipe(
D.readFile(filename),
D.chain((s) => D.writeFile(filename, f(s)))
)
return pipe(
D.readFile('file.txt'),
D.chain(D.log),
D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
D.chain(() => D.readFile('file.txt')),
D.chain(D.log)
)
}
// -----------------------------------------
// `Deps` 인스턴스 (수정됨)
// -----------------------------------------
import * as fs from 'fs'
import { log } from 'fp-ts/Console'
import { chain, fromIO } from 'fp-ts/Task'
const DepsAsync: Deps = {
readFile: (filename) => () =>
new Promise((resolve) =>
fs.readFile(filename, { encoding: 'utf-8' }, (_, s) => resolve(s))
),
writeFile: (filename: string, data: string) => () =>
new Promise((resolve) => fs.writeFile(filename, data, () => resolve())),
log: (a) => fromIO(log(a)),
chain
}
// 의존성 주입
program5(DepsAsync)()
문제 이전 예제에서는 일부러 발생 가능한 오류를 무시했습니다. 예를들면 작업 중인 파일이 존재하지 않을 수 있습니다. 이를 고려해 FileSystem 효과를 어떻게 수정할 수 있을까요?
import { Task } from 'fp-ts/Task'
import { pipe } from 'fp-ts/function'
import * as E from 'fp-ts/Either'
// -----------------------------------------
// 프로그램의 효과 (수정됨)
// -----------------------------------------
interface FileSystem<A> extends Task<E.Either<Error, A>> {}
// -----------------------------------------
// 의존성 (수정 안됨)
// -----------------------------------------
interface Deps {
readonly readFile: (filename: string) => FileSystem<string>
readonly writeFile: (filename: string, data: string) => FileSystem<void>
readonly log: <A>(a: A) => FileSystem<void>
readonly chain: <A, B>(
f: (a: A) => FileSystem<B>
) => (ma: FileSystem<A>) => FileSystem<B>
}
// -----------------------------------------
// 프로그램 (수정 안됨)
// -----------------------------------------
const program5 = (D: Deps) => {
const modifyFile = (filename: string, f: (s: string) => string) =>
pipe(
D.readFile(filename),
D.chain((s) => D.writeFile(filename, f(s)))
)
return pipe(
D.readFile('-.txt'),
D.chain(D.log),
D.chain(() => modifyFile('file.txt', (s) => s + '\n// eof')),
D.chain(() => D.readFile('file.txt')),
D.chain(D.log)
)
}
// -----------------------------------------
// `Deps` 인스턴스 (수정됨)
// -----------------------------------------
import * as fs from 'fs'
import { log } from 'fp-ts/Console'
import { chain, fromIO } from 'fp-ts/TaskEither'
const DepsAsync: Deps = {
readFile: (filename) => () =>
new Promise((resolve) =>
fs.readFile(filename, { encoding: 'utf-8' }, (err, s) => {
if (err !== null) {
resolve(E.left(err))
} else {
resolve(E.right(s))
}
})
),
writeFile: (filename: string, data: string) => () =>
new Promise((resolve) =>
fs.writeFile(filename, data, (err) => {
if (err !== null) {
resolve(E.left(err))
} else {
resolve(E.right(undefined))
}
})
),
log: (a) => fromIO(log(a)),
chain
}
// 의존성 주입
program5(DepsAsync)().then(console.log)
데모